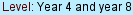number
 : Numbers in Squares
 68k
Approach: Team
Resources: 50 plastic beans; sample number square (A4 size); 2 number squares (A3 size).

Questions / instructions:
Show students sample number square.
On this number square you can see that A and B are added to give 9; C plus D equals 16; A plus C equals 11; A plus D equals 13, and so on. The four numbers in this square have been added down, across and diagonally, and the sum of each addition is shown.

  % responses
y4
y8

Show number square 1. Put beans and pencils on table.
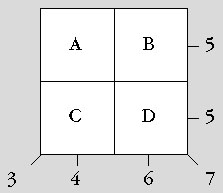1. I want you to work together to try to work out the numbers that should go in A, B, C and D. You can put these beans in the squares and move them around to help you find the answer or you may write in the squares. You will need to try to work out a strategy for solving the problem. Tell me when you are finished. Check your additions. Then write and circle your final answers in the squares.
Problem solved
67
99
How problem was solved:
collaboratively (3–4 students)
76
86
two students
16
9
one student, others watching
6
5
Evidence of: sophisticated strategy
3
6
systematic strategy
7
15
random trial and error
83
87

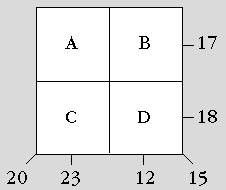Now here is another number square.
Give them number square 2.
2. Now work together again to try to work out the numbers for these squares, then write your answers in the squares and check them. Put a circle around your answers.

Problem solved
38
82
How problem was solved:
collaboratively (3–4 students)
74
88
two students
16
8
one student, others watching
9
3
Evidence of:
sophisticated strategy
0
9
systematic strategy
7
26
random trial and error
79
93

When the second number square has been solved say:
3. If you were helping another team to work these out, what would you tell them?
Strategy suggested:
based on the pattern of numbers
5
13
based on systematically trying different options in one cell
0
33
random trial and error
27
54

Sophisticated strategy: based on the pattern of numbers given (eg., this cell must have large number)
Systematic strategy: based on adjusting one cell through possible options

    
Commentary:
Year 8 students were much more successful than year 4 students. Few teams adopted strategies based on systematically varying the number in one cell, or on looking at the overall pattern to see whether a cell was likely to have a large or small number (eg., cell C in square 1 will be a small number because the totals involving cell C are small). By the time they answered question 3 almost half the year 8 teams had identified such strategies as useful.

[ top of the page | Maths Assessment Report 1997 ]