Name
of activity |
Place
value knowledge or skill |
ENP
group (5 children) |
NEMP
group (4 children) |
| Girls and Boys | Showing multi-digit numbers with place value blocks | all
|
all |
| Population | Reading a 4-digit number (2495) | all
|
3 |
| Number C | Writing a 4-digit number | all
|
all |
| Number C | Writing a 6-digit number | 2
|
0 |
| Population | Knowledge of all positional values in 2495 | 4
|
2 |
| Calculator | Ordering Ordering numbers | all
|
all |
| Girls and Boys | Dividing an even number into two groups with place value blocks | 4
|
3 |
| Girls and Boys | Dividing a number using regrouping with place value blocks | 3 |
1
|
| Speedo | 1996 + 1 | 4
|
3 |
| Speedo | 1996 + 10 | 2
|
1 |
| Speedo | 1996 + 100 | 2
|
1 |
| Speedo | 1996 + 1000 | 2
|
2 |
| Speedo | 3402 – 1 | 4
|
2 |
| Speedo | 3402 – 10 | 2
|
1 |
| Speedo | 3402 – 100 | 3
|
1 |
| Speedo | 3402 - 1000 | 3
|
2 |
| Number order | Arrange four digits to make smallest possible number | all
of 3 recorded |
3 |
| Number order | Arrange four digits to make largest possible number | 2
of 3 recorded |
3 |
| Number A | 700 + 100 | all
|
all |
| Number A | 15 735 + 100 | all
|
3 |
| Number B | 400 - 100 | all
|
2 |
| Number B | 643 - 100 | all
|
2 |
| Number C | 6 x 10 | all
|
3 |
| Number A | 12 x 10 | all
|
2 |
| Number C | 78 x 10 | 1
|
1 |
| Number A | 316 x 10 | 1
|
2 |
| 36 + 29 | Adding 36 + 29 | all
|
3 |
| Motorway | Problem-solving (estimating 9 x 98) | 1
|
1 |
| NEMP activity | ENP children | NEMP children | ||||||||
| 36 + 29 | A |
B |
C |
D |
E |
A1 |
A2 |
A3 |
A4 |
|
| Method used by the children to solve this problem |
|
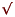 I’d take away the 9 and 6 and add 20+30=50 and put on the 9+6 then it would be 65. SPLIT |
Gave 65. Explained that she added 30+20=50 and 9+6=15 so 50+15=65 SPLIT |
Gave 65,smiled and said that… 9+6=15 and 2+3=5 (adding in tens) and that equals 65. SPLIT |
After a long think she gave 65 and explained… 36+10=46 plus ten equals 56 plus 9 is 65. JUMP |
x 3+2=5 (adding tens) and 9+6=15 so…515. |
30+20=50 add on..repeats 9+6=15 … add on… the answer’s 65 SPLIT |
it’s 65,put 29 under 36, add 6+9=15 put down 5 carry one, 1+3 is 4 and 2 is 6 Algorithm method |
3+2 = 5 and 6+9 = 15 put it in working form, 9+6=15 put 5 down, carry 1 to 3,4+2=6…65 Algorithm method |
|
| Other strategies | Another version of the above method where 50+15=65 | No
|
No
|
No
|
No
|
No
|
No
|
No
|
No |
|
Notes: ENP
children
1. Split method dominant
2. Confident use of this mental strategy
Notes: NEMP
children
1. Algorithms well established as a mental strategy
2. No other strategies
| NEMP activity | ENP children | NEMP children | ||||||||
| Calculator Ordering | A | B | C | D | E | B1 | B2 | B3 | B4 | |
| Arranged in order correctly | y | y | y | y | y | y | y | y | Omitted from tape | |
| Read
the numbers 14 41 104 140 4010 4100 |
y | y But read 4100 as 400 and 401 then as 4001 finally as 4100 |
y | y | y but read 4100 as 4400 initially then correctly |
T/A
forgot to get her to read the answers |
Read
4100 as 400 then asked for if that was right. |
y | Omitted from tape | |
Notes:
ENP children
1. The question was unclear to some children; C needed some prompting
to move the cards around before she established the right answer.
2. B needed some time to process the answer
NEMP children
3. B2 could read 4010 but not 4100. She knew 2 and 3-digit numbers and
recognised the increasing size of digits.
| NEMP activity | ENP children | NEMP children | ||||||||
| Girls & Boys | A | B | C | D | E | C1 | C2 | C3 | C4 | |
| Make 26 with blocks | |
|
|
Tried to use all of the blocks as ones initially |
|
|
|
|
|
|
| Is it possible to have equal girls and boys in this class? | |
|
|
|
not sure | |
|
|
|
|
| Show what two equal sets from 26 would be | |
Picks one rod and takes away three. There would be 16 boys and 16 girls. Changed this to 13 because 16 was “too big” |
Says she figured it out with her fingers. |
Says he just “knew” that 13 was half of 26 and could not explain further. |
Not sure | |
x Did not use the 26 that he had made up at first. Said 14 was the answer as 14+12=26; then gave 28 as the sum of 14 and 14. |
|
|
|
| Make 32 with blocks | |
|
|
|
|
|
Made shape of
32 first. |
|
|
|
| Is it possible to have equal girls and boys in this class? | |
Explains…15+15=30
and 1+1=2 so 16 is the answer. Initially could not see how
to use blocks to make 16+16. Prompted, managed to make 2 groups of
16. |
|
|
not sure | |
At
first said no because there are “normally more girls
than boys in a class”. |
|
x Because 3 is not an even number |
|
| Girls
& Boys (continued) Show what two equal sets from 32 would be |
Did not regroup with blocks. Said 16+16=32 because 2x10=20 and 2x6=12 which makes 32. |
|
not sure | |||||||
Notes:
Early Numeracy Project children
1. A and B both used the split method to work out half of 32. 10+10=20
and 6+6=12 which makes32 therefore the answer is 16; or 15+15 =30 and
1+1=2, therefore 15=1=16. B couldn't work it out initially with blocks
which may support the suggestion in Note 1.
2. D used the blocks as single units initially and then, once prompted,
remembered and used them in the correct manner but then over-ruled his
own correct answer.
NEMP children
1. Used place value blocks confidently to make up 26 and 32; C1 attempted
a split method and came close to the correct answer.
2. C2 tried a split method but confused division with multiplication;
C3 exchanged a ten block for a set of 10 ones and showed the correct answer.
3. C4 got stuck on 3 tens being an odd number and therefore not divisible
by 2.
| NEMP activity | Early Numeracy Project children | NEMP children | ||||||||
| Independent | A | B | C | D | E | A1 | A2 | A3 | A4 | |
| Number A | ||||||||||
| 700 + 100 | |
|
|
|
|
|
|
|
|
|
| 15 735 + 100 | |
|
|
|
|
n/a | |
|
|
|
| 12 x 100 | |
|
|
|
|
n/a | 112 | |
|
|
| 316 x 100 | 4060 | no attempt | 4060 | |
4060 | n/a | 416 | |
|
|
| Number B | ||||||||||
| 400-100 | |
|
|
|
|
|
100 | |
100 | |
| 643 – 100 | |
|
|
|
|
|
364 | |
143 | |
| Number C | ||||||||||
| 6 x 10 | |
|
|
|
|
0.6 | |
|
|
|
| 78 x 10 | 150 | 700 | no attempt | |
156 | 1.91 | 70 | |
150 | |
| write in figures | ||||||||||
| five hundred and eighty | |
|
|
|
|
|
|
|
|
|
| two thousand five hundred and eighteen | |
|
|
|
|
|
|
|
|
|
| two hundred thousand and forty three | |
2340 | no attempt | |
2243 | n/a | 2000043 | 2.140 | 2043 | |
Notes:
ENP children
1. Adding and subtracting 100 well established
2. Multiplication of a 3-digit number by 10 was difficult for most; curiously
same incorrect result for three children.
3. Could all write 3 and 4 digit numbers correctly.
4. Starting to establish multiplying of 10 and 100 correctly.
NEMP children
1. Adding 100 was established; most were successful with adding 100 to
a 4 digit number.
2. Subtraction less secure than adding 100; subtracting century similar
results.
3. 3 and 4 digit numbers well known; thousands concept and how it is written
is not established yet.
| NEMP activity | ENP children | NEMP children | ||||||||
| Motorway | A | B | C | D | E | A1 | A2 | A3 | A4 | |
| estimate 9 x 98 | 966…I just thought that if 98 + 98 is… then used split method to work out 196 … and I thought it would be quite big so got about 900. |
x 188…I started with 98 and went all the way up to 188 |
x Not sure. When I gave the prompt that 98 was close to a number that might make it easier she got 100 when asked what 9 X 100 was she got 900 then 995. |
x long thinking…166 because he used 9x8 and 9x9 = (72 + 81) |
x 20…why? …I guessed |
x Looking at T/A …smiles and says 98x9. T/A asks for an estimate. Says 500. T/A asks How did you get that? I guessed…I did 9x95 it was too big so I just guessed |
x T/A repeats question. Says 1000 and … looks away…100+26 or 24…T/A asks how did you get that? I just worked out that there would be 80…98… child did not explain any more. |
x 8172… T/A asks for an explanation I multiplied 8x9 then 9x9 |
T/A repeats question Whispering to herself… it’s 882…I timesed 9x98 |
|
Notes:
ENP children
1. This seemed a difficult one for most of the children.
2. Evidence of trying to use the split method to work it out by B; D tried
to use the algorithm method.
NEMP
children
1. Mental algorithms attempted by all children, only A4 was successful.
A3 multiplied correctly but could not rename.
| NEMP activity | ENP children | NEMP children | ||||||||
| Number Order | A | B | C | D | E | A1 | A2 | A3 | A4 | |
| Arrange the digits 3 ,5, 8, 1 to make the smallest possible number | |
|
lost this section of tape | lost this section of tape | 1835 read it correctly |
x Adds 5+ 8=13 Unsure T/A prompt “Is that the biggest number you can make using all of the cards? Still unsure |
|
|
Initially unsure and starts to add 3 + 5 then multiplies 3x5=15 ..=8 is 23 +1 = 24 |
|
| Read 1358 | |
|
lost | lost | x | |
|
|
||
| Arrange the digits 3 ,5, 8, 1 to make the biggest possible number | |
|
8351 read it correctly | Not sure of the question | |
|
Gets it and also changes answer to previous question |
|||
| Read 8531 | |
|
lost | lost | x | |
|
|
||
ENP children
1. This seemed to be an easy activity for the children
NEMP children
1. The question caused some confusion with A1 and A4. They both thought that they were being asked to add the digits together.
| NEMP activity | ENP children | NEMP children | ||||||||
| Population | A | B | C | D | E | B1 | B2 | B3 | B4 | |
| Read 2495 | |
|
|
|
|
|
249…no… 24095 | |
|
|
| place value of 4 | |
|
Needed the question clarified first. |
|
40 | 100s um…400 |
x It’s the second number. |
|
Do you
mean like what column is it in? T / A repeats question…4 tens |
|
| place value of 5 | |
|
|
|
|
|
x It’s the last number so that’s what everything has. |
|
x one… I don’t know |
|
| place value of 9 | |
|
|
|
9 | tens |
x not sure |
|
x one…not sure |
|
| place value of 2 | |
|
|
|
2 | |
x
not sure |
|
2000 |
|
ENP children
1. “What does (the number) stand for?” was not initially understood by children who later answered the question correctly.
2. Is the prompt in the NEMP manual unclear? E read “2” for the value of the 2 in 2495 and when asked how she got that explained that it was in the thousands column which would suggest that she understands more about place value than the question reveals.
NEMP children
1. Two children had difficulty understanding the question; B4 knew that the 2 was 2000 so she may have understood the other questions if she had been asked in another way.
| NEMP activity | ENP children | NEMP children | ||||||||
| Speedo | A | B | C | D | E | A1 | A2 | A3 | A4 | |
| 1996 + 1 | |
3906 | |
|
|
|
3224 | |
|
|
| 1996 + 10 | |
12906 | 1916 | |
2060 | 1916 | 9999 | 1906 | |
|
| 1996 + 100 | |
no attempt | no attempt | 2996 | |
1600 | 99999 | 2006 | |
|
| 1996 + 1000 | |
no attempt | no attempt | |
no attempt | 6000 | 400999 | |
|
|
| 3402 - 1 | |
4804 | |
|
|
3403 | 4402 | |
|
|
| 3402 - 10 | |
13804 | no attempt | unclear | |
3412 | 12402 | |
not attempted | |
| 3402 - 100 | |
no attempt | no attempt | |
|
3100 | 100402 | |
3300 | |
| 3402 - 1000 | |
no attempt | no attempt | |
|
2000 | 100402 | |
|
|
ENP children
1. Why use 1996 for the addition question? It involves two steps: adding and renaming as well for adding 10 and 100.
2. Why use 3402 for the same reason? Renaming with the take away ten question.
3. Suggest using 1546 and 3547 as questions that have only the place value component and do not rely on renaming as well.
NEMP children
1. Achieved slightly above the NEMP (2001) report results.
2. A wide range of answers given, with some six-figure numbers that showed a lack of understanding of larger numbers.
