INTRODUCTION
In this research we set ourselves the challenge of clarifying ideas about progression in the development of children’s investigative skills. Our initial intention was to compare the actions of Year 4 and Year 8 children, as described in the previous section, with the model of progression represented on the Exemplars Matrix. However, as the research has unfolded we have also searched for reports of investigations from the fields of cognitive psychology and science education in which researchers have aimed to describe and explain various patterns in the development of children’s investigative skills.

Our purpose in comparing these different sources of information has been to think critically about what progression actually entails. We also wanted to locate and summarise findings that might give classroom teachers useful ideas for actively developing the investigative skills of the children they work with. These intentions have, however, highlighted a tension that exists in any efforts to exemplify children’s work in a staged manner that compares children of the same/different stages and ages. Should such comparisons be based on what the “average” or “normal” child can and does do, or on what is possible for children who are fortunate enough to experience specific types of exemplary teaching?

This tension is not easily resolved. If naturalistic observations are taken as a basis for comparison, then observations of actual children working on science investigations should be the most important source of information. Our NEMP analysis obviously fits this method of investigation, as does the Exemplars project. This “common sense” way of approaching developmental issues is not, however, unproblematic. Contemporary science philosophy emphasises the theory-laden nature of observations (Chalmers, 1982). What we attend to when observing children in the process of carrying out investigations very much depends on the theories of progression that drive our thinking. If these theories are taken for granted, we are in danger of assuming an obviousness to development that limits the possibilities for challenging what might be achieved with different types of teaching. To help tease out this issue, some ideas central to theories of progression are briefly discussed in the first sub-section below. Following that, research that does attempt to develop specific and explicit theories of progression in the development of science investigation skills is summarised.

THE NATURE OF “PROGRESSION” IN SCIENCE LEARNING
We expect children to make progress in their learning during their years at school. We expect teachers to “make a difference” to that progress, and to effectively enhance children’s natural tendencies to learn. However, we have already noted that there are differing ways in which progression can be viewed. This sub-section highlights some theoretical ideas that underpin various common models of progression, with a particular focus on those views that are likely to be taken for granted as “common sense”, and perhaps only recognised in hindsight (Barker, 2000). These are the views that would seem to be in particular need of examination, if ideas about progression are to be rethought by curriculum developers, classroom teachers, and those who monitor and evaluate the results of teachers’ work.

Learning theories and progression
Theories of learning frequently inform views of progress. Some views of progression are focused more on the “breadth” and “extent” of children’s knowledge — that is, they take quantitative “knowledge acquisition” models of learning. Other views are premised on more qualitative “conceptual change” models of learning (Harrison, Simon, and Watson, 2000). The “acquisition” models align with behaviourist (building block) or developmental (staircase) theories of learning, while the “change” models align with constructivist theories of learning (Biddulph and Carr, 1999). More ecological theories of learning (humanistic and enactivist), as also outlined by Biddulph and Carr, raise quite different types of questions about purposes for learning science, and may align with ideas of progression centred around changing goals for science education at different stages of schooling (Fensham, 1994). These ecological theories are not discussed further in this section because the focus of this report is very much on the development of traditional types of classroom-based science investigations.

Behaviourist and developmental theories of learning typically derive their progressions from the “internal logic of the academic disciplines of science, as they have developed, particularly conceptually since the mid 20th century” (Fensham, 1994, p. 79). Such progressions are ordered according to what is seen as the logical order of development of subtopics, with curriculum organisation based on criteria such as a move from simple relationships to complex patterns, or concrete experiences to ideas that involve abstract logical thinking. Constructivist theories of learning may lead to progressions based on conceptual change research, so that the focus moves from the logic of science to patterns of children’s thinking and subsequent next learning steps (Harrison et al., 2000). Frequently, curricula are structured in ways that present an amalgamation of these two different approaches.

Developmental theories and progression
Progression can be theorised as having a developmental basis. In this view children are not “ready” for particular sorts of learning until they have reached some physical and/or psychological maturation stage. This has been described as a “folk theory”, albeit one that is still widely held amongst the teaching profession (Watson, 1996). Watson reviews recent research concerning the nature and potential of young children’s learning to describe a quite different type of view from the folk idea of “readiness”:

Readiness, on this [new] view, thus requires that children recognise beliefs qua beliefs — that is, as not synonymous with reality and subject to revision. The revision of belief is a domain-general, metarepresentational ability that lies at the very core of intentional learning. It underlies the child’s ability to intentionally enrich or change the core explanatory principles in a naïve theory, and thereby, the ability to learn from formal instruction (Watson 1996, p. 160).

Here the formal theory-based ways of thinking practised by scientists have been compared in essence with the processes that children follow as they revise and expand their mental models and schemas. This view of “readiness” potentially aligns with constructivist and/or ecological theories of learning, drawing attention to the importance of metacognitive as well as the cognitive thinking. Progression is premised on the concept that children think in “theory-like” ways from a young age – something that has been borne out by recent research with very young children (Watson, 1996).

These new biological insights raise important challenges to widely-held Piagetian notions of stages of mental operations that have strongly influenced the way in which children’s learning in science has been structured in the past. Piaget’s ideas, in particular the notion of a “formal operations” stage of development, have arguably formed an important, often implicit, part of the theoretical framework within which both curriculum itself and observations of children’s actual learning achievements have been assessed and interpreted since the middle of the twentieth century. However, Metz (1995) mounted a strong critique of the Piagetian position. If students are shielded from experiences that will foster their awareness of warrants for their own beliefs, on the grounds that such ideas about their experiences are as yet too abstract, they cannot begin to gain key skills needed to appreciate the specific ways of thinking involved in “being scientific”. Where teachers do not expect that students could make such progress at a relatively young age, “folk theories” of readiness become self-fulfilling in the limitations placed on children’s learning opportunities.

The point just made returns us squarely to the tension between an “exemplary” model of progression, that demonstrates what children could achieve, and a more “naturalistic” one that orders what children typically do achieve at various ages as they experience conventional models of teaching and curriculum. The framework presented in Section Five draws partly on research that presents evidence that children can achieve much more than is typically expected of them – but only if they are exposed to the sorts of constructivist models of learning that foster their personal epistemological development. However, we have attempted to side-step the normative/exemplary dilemma by avoiding the use of “level” numbers or age-group alignments, instead giving the 5 identified framework clusters names that we hope fairly reflect their overall place in the sequences of progressions. We have done this partly to avoid confusion with the idea of curriculum levels, but also because we want to emphasise that this is a developmental sequence where any one stage might be applicable to students of a wide range of ages, depending on their previous learning experiences. Equally, any one student is likely to vacillate at the boundaries of two stages during transition times, sometimes showing characteristics of one, sometimes of the other.

Fensham (1994) makes the point that frameworks that seek to unify views of progression across the entire school curriculum are a phenomenon of the late 1980s and beyond. Before that time, he suggests, views of purposes for learning, and thus beliefs about what constitutes progress, were perceived quite differently at different stages of schooling. The Exemplars Matrix mainly seeks to exemplify teaching and learning at primary school levels, and is restricted to Levels 1–5 of SNZC. Its developers were certainly aware that the purposes for science teaching perceived by primary teachers can be very different from those perceived by secondary teachers (Coles, MacIntyre, and Radford, 2001). Whether the Exemplars Matrix could be extended right through all the levels of the curriculum is an interesting matter for debate.

The meta-level framework presented in Section Five develops descriptors for learning continua that arguably extend from earliest school learning right up to undergraduate university study. We felt it was important to do this because the interplay between ideas (whether children’s own ideas or scientists’ ideas) and the development of children’s investigative skills is something that we believe is in need of critical attention. The analysis we have undertaken suggests that thinking and reasoning within coherently developed frameworks of scientifically correct theories only become important in the final stage – that is at the upper levels of secondary schooling and beyond. Fensham’s alternative model of progression, slanted towards a “science for all” view of purposes for learning, also emphasises a “solid foundation” [of scientifically accurate theories] only at the upper secondary level (Fensham, 1994). This seems to us to free the way for rethinking the emphasis on content at lower curriculum levels, something that has been widely advocated in recent international discussion of reform in science education (see, for example, Millar and Osborne, 1998; American Association for the Advancement of Science, 2001).

THEORETICAL SUPPORT FOR THE FRAMEWORK
In seeking to design this developmental framework, we have drawn heavily on research. One paper proved particularly helpful in providing a starting point for reflecting on what primary school children can achieve if freed from prevailing expectations of “normal” development. Smith, Maclin, Houghton, and Hennessey (2000) compared 2 grade six classes of American students who were closely matched demographically. One group of children had been exposed to a constructivist science education programme from the outset of their schooling. The same teacher had worked with these students every year, during 3 hours of science learning time per week, with the aim of developing in every student a metacognitive awareness of theory building as personal learning process, as well as the primary goal of scientific inquiry. Teaching that could achieve such aims was described in Chapter Five of the recent literature review on effective teaching to raise achievement for all New Zealand students in science (Hipkins et al., 2002). The other class was taught by a teacher who took a keen but more conventional interest in science learning, focusing on the “Science Fair” as an important culminating goal for student investigations. The research team carried out “nature of science” (NOS) interviews with each child from both classes, using previously validated semi-structured interview questions, and the results were analysed within a careful framework that allowed for inter-rater validation.

From these results, Smith et al. (2000) described a developmental sequence of children’s understandings of the nature of scientific inquiry. They described 3 levels in the development of children’s understanding, with transitions between these characterised as level 1.5, and level 2.5. In their sequence, level 1 represents a naïve “knowledge unproblematic” view of science, and level 3 represents a sophisticated and well-developed epistemology that reflects contemporary “knowledge problematic” thought about the provisional nature of science theorising. The details of this developmental sequence have made a significant contribution to the shaping of the framework presented in Section Five. Specifically, the columns headed “meta-level view of knowledge”, “personal knowledge skills”, “view of scientists” goals/methods”, and “personal meta-values” were initially collated using data drawn from these research findings and the associated discussion. Some aspects of the column “meta-level view of investigations” were also drawn from this research, especially for the first 3 clusters.
Smith et al. (2000) found that students from the constructivist classroom averaged level 2 or above on the developmental sequence they had devised, while those in the traditional classroom averaged between level 1 and level 1.37. They found very little overlap between 2 groups, in any of the categories that they developed. The diagrams they developed to represent a “modal epistemology” for each group vividly illustrate the richness of the nature of science thinking that had been developed by the children in the constructivist classroom, compared with the children in the traditional classroom. We have redrawn these diagrams for presentation below. Note the richer links and deeper NOS ideas of the children in the “science as knowledge building” classroom (Figure 2). The centrally linked idea of knowledge building as a collaborative activity is completely missing in the NOS understandings of the children in the traditional classroom (Figure 1).

Figure 1
A “modal epistemology” for sixth grade students in a traditional American class

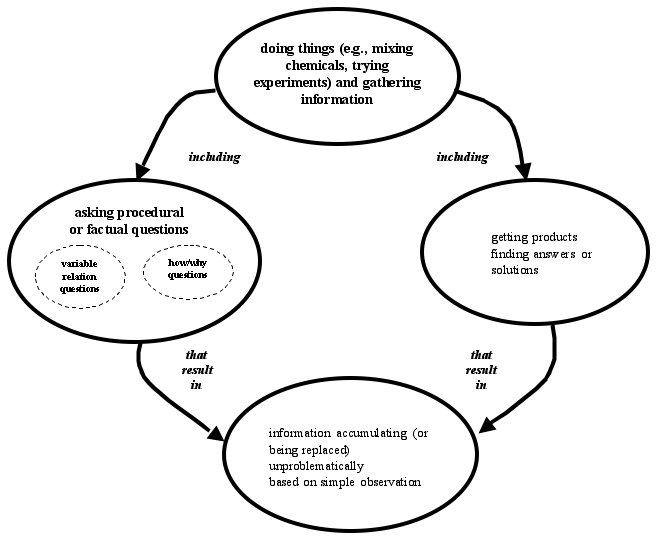
Source: Smith et al., 2000, p. 382

Figure 2
A “modal epistemology” for sixth grade students who had experienced teaching with a specific focus on knowledge building processes

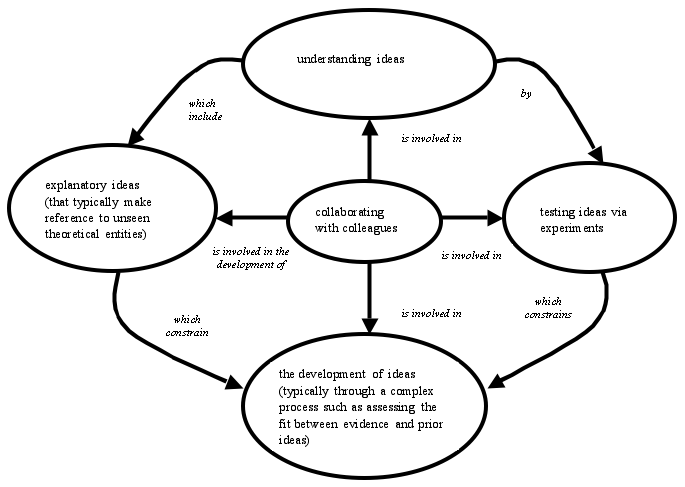
Source: Smith et al., 2000, p. 381

Their findings lead these researchers to suggest that the achievement record of the students in the constructivist classroom “need not be limited to just a few precocious sixth graders, but is well within the grasp of an entire classroom of students” (Smith et al., 2000, p. 398). Level 2 of their sequence is represented as the third cluster of our framework: A developing sense of knowledge testing. This was the lower level of achievement for one class but above the level of achievement of all the students in the other class Smith et al. researched. Tellingly, these researchers suggest that the main factor preventing some of the “constructivist classroom” students from achieving the top level (level 3) of their scheme was that they did not yet hold a coherent and overarching framework of science explanatory knowledge. As they pointed out, students cannot be expected to develop such frameworks at least until their senior years of secondary school. Nevertheless, it is food for thought that these still relatively young students, as a whole class, achieved what traditional views of progression might judge as being beyond many junior to mid-secondary students.

In a critical review of research on children’s NOS understandings, Hogan (2000) alerts us to a potential gap in our knowledge of children’s development if they are only asked about their ideas of scientists’ science. Such knowledge is declarative – a distal knowledge that may or may not influence the way in which children carry out their own science investigations (that is, their proximal NOS knowledge). The analysis of the NEMP tapes, reported in Section Three, illustrates how children often do much more than they say when carrying out investigations, so the distal/proximal distinction could make a significant difference to the way ideas about progression in children’s learning are interpreted and ordered. With this caution in mind, we note here that, while Smith et al. (2000) do report children’s comments on their own investigative work, the interview questions primarily address their distal knowledge – that is “what scientists do”, which does not necessarily connect to what children actually do. To address this issue, we next aligned the preliminary framework clusters with research findings from projects that describe progressions in what children actually do when they carry out their own science investigations.

THE ROLE OF MENTAL MODELS IN PROGRESSION
Kuhn, Black, Keselman, and Kaplan (2000) provide a different but complementary perspective to the research of Smith et al. Kuhn and her colleagues were also interested in the impact of meta-levels of cognition on children’s progress. They hypothesised that success in learning via active inquiry may be promoted or hindered by the mental model of causality currently held. In this view, constraints on children’s ability to progress could be top-down rather than the more usually considered bottom-up constraints posed by the limitations to the actual learning experiences provided. Kuhn et al. (2000) tested their hypothesis via the development of a computer simulation that tracked children’s decision making when solving problems that involved discerning which were the causal variables in a multivariable “real world” context. The task involved determining the causes of flooding in a simulated lake by running trials of different variable combinations and levels (e.g. water temperature = hot or cold: soil depth = deep or shallow). The researchers acknowledge that “mental models of any sort remain essentially unobservable theoretical constructs” (p. 516). However, they present the patterns of responses made by the children as evidence that supports the existence of a developmental sequence of mental models of causality.

At the beginning of this developmental sequence children focus exclusively on outcomes – if an event is triggered and a certain outcome occurs, then the two are directly and unproblematically related to each other. With a mental model such as this each investigative episode has its own discrete outcomes and the idea of controlled comparisons between adjacent events has yet to be developed. During the NEMP tape analysis we certainly saw many instances where this type of thinking appeared to be in operation, and we have described some of these in Section Three. While other explanations for this type of “discrete episodes” response can be proposed (for example, limitations of memory space – see below) this mental model does appear to align strongly with the naïve, “knowledge as true facts” view described as the beginning of the developmental sequence of Smith et al. (2000). With this juxtaposition we began the alignment of Kuhn et al.’s research with the emergent clusters of the framework.

Kuhn et al. (2000) contrast the outcomes-focused mental model just outlined with what they call an analysis model. As this new mental model gradually develops children come to recognise that there can be a relationship between separate variables, and this in turn is associated with the realisation that it is necessary to think more carefully about the actual cause of a particular outcome. Children will begin to demonstrate their emergent development of an analysis mental model when they correctly choose between possible variable combinations to identify unconfounded “fair tests”. Emergent “analysis” from this mental model perspective seems to us to align readily with “explanation” from the epistemological perspective of Smith et al. (2000) and so the second framework cluster also falls into alignment. (This emphasis on choosing — as opposed to actually producing/designing/planning — seems itself to be significant as a developmental step and will be further discussed below.)

Kuhn et al. (2000) then describe several subsequent developmental stages of the “analysis” mental model of causality. Children progress as they learn to discern the separate effects that two or more variables may exert on an outcome – an additive stage. They are beginning to show a “metastrategic understanding” (p. 513) as demonstrated by their ability to give a simple explanation for why one potential “fair test” is better than another. We did not see any evidence of this type of thinking during the NEMP task re-analysis. However, we also note that the tasks presented, while having the potential for multivariable analysis, were not developed and presented to the children in a manner that would allow them to display such thinking.

This “additive outcomes” mental model seems to us to align with the notion that scientists need to “test ideas”, as characterised in the next developmental stage described by Smith et al. (2000). Later still, the additive mental model can develop into a more interactive model as children expand their repertoire of experiences of situations to include more complex episodes where variables affect the outcome in some combined way (as potentially seen in the Ball Bounce task). Children who are working with investigations at this level will recognise a need to manage two or more independent variables simultaneously, something that has also been associated with progression by science educators who have taken a “task based” approach to their theoretical reasoning (Gott and Mashiter, 1994). While the link is more tenuous, it could be argued that this stage aligns with the idea that evidence has the potential to disconfirm theories – an idea that is identified at the fourth level of Smith et al.’s epistemological developmental sequence. This potential link will be further explored through the research projects of Chinn and Malhotra (2002), and of Zohar (1995) and her colleagues, that are introduced below.

The final step in Kuhn’s developmental sequence of mental models of causality introduces the development of more complex interactive mental models where multiple possible pathways to outcomes must be taken into account. Kuhn et al. (2000) note that this opens up the possibility that the co-ordination of theory with new evidence can proceed in several different ways and hence it is necessary to represent evidence independently of theory as far as is possible – a skill that they identify as “the hallmark of mature or skilled scientific thinking” (p. 519). This seems to us to align with the overarching explanatory frameworks for scientific theories that Smith et al. (2000) identify as a key feature of their “level 3” students. In all likelihood, many school students will never reach this level. The nature of appropriate learning opportunities that can help students develop their metacognitive awareness of data evaluation is still a matter of debate in the research community (Chinn and Brewer, 2001) and we have not developed this aspect further in this report.

LEARNING ABOUT “FAIR TESTING”
Researchers from the cognitive psychology field have given quite detailed attention to the manner in which children learn to manipulate investigations using controlled variable strategies (known in this literature as CVS investigations). Such strategies are given considerable emphasis at the primary school levels of SNZC, where they are denoted by the use of the phrase “fair testing”. This type of investigation has been defined as one in which “students decide to change an independent variable, observe the effect on a dependent variable, and control other key variables” (Watson, Goldsworthy, and Wood-Robinson, 2000, p. 71). All 3 investigations reported in Section Three anticipated “fair tests” of this sort as the appropriate means of carrying out the set task.

The notion of “fair testing” has proved to be a powerful metaphor. This approach to science investigations has been widely adopted amongst teachers. Science education research in the UK has shown that, at least at the primary school level, this has been to the detriment of the development of children’s knowledge of other forms of scientific investigations. Furthermore, these researchers report of a very narrow range of contexts in which such investigations are typically carried out, with 30 percent of all the investigations using just 4 contexts: thermal insulation, dissolving, pulse/breathing rate with exercise, and friction (Watson et al., 2000). Watson and his colleagues express concerns about the NOS messages implicit in this narrow focus on just one type of investigation, and point out that such experiences also provide inadequate opportunities for children to learn about the relationships between the development of scientific theories and empirical evidence. These concerns reinforced our belief that fair testing warranted close scrutiny as we shaped our developmental framework. The research reported next has particularly influenced our thinking about how the framework clusters can be used to encourage active teaching that leads to progress in the development of “fair testing” science investigative skills.

Differentiating between choosing and carrying out
When presented with simple choices, young children can recognise “fair” (unconfounded) CVS tests even if they are not yet able to justify their choices (Kuhn et al., 2000), and well before they can actually produce such tests for themselves. Schauble (1996) cites a range of studies where this has been confirmed. A rare longitudinal study of one cohort of German children, that tracked their development across the primary school years, also confirms this pattern (Bullock and Ziegler, 1999). These researchers suggest that the distinction provides important new insights into children’s developing investigative skills:

..when children are asked to produce experimental tests, their performance suggests that they do not understand the logic of experimental control. In contrast, when children are asked to choose a controlled test, their performance at least by fourth grade suggests that they do understand the logic of experimental control. Furthermore, and this is important, of those who chose controlled tests, more than 50% of the fourth graders, about 80% of the fifth graders, and almost all of the sixth graders also justified this choice in terms of controlling variables, suggesting that their understanding is also somewhat explicit (Bullock and Ziegler, 1999, p. 45).

It seems to us that making choices has been a neglected factor in descriptions of progression, and we identify it as a focus for the active teaching of investigative skills to children who seem to be located developmentally within any one of the first 3 clusters described within our framework. We cannot report on this ability from our observations of the NEMP tasks because the children were required to actually produce fair tests in all 3 tasks. It seems to us that it would be a relatively simple matter to design NEMP tasks and other learning materials that provide examples where children choose the “fair test” from pairs or sequences provided to them, and then discuss the reasons for their choices. Furthermore, the work of Kuhn et al. (2000) suggests to us that choosing and justifying those choices form a progression of their own, with the increasing ability to explicitly justify choices in terms of CVS strategies linked with the development of more sophisticated mental models of causality.

Thinking about variables during investigations
Clearly, children do also show progression in their ability to produce fair tests. Chen and Klahr (1999) investigated changes in children’s ability to produce fair tests after explicit instruction. They found that the youngest children in their study (American grade 2) improved marginally after instruction but had difficulty remembering the skills they had been taught when transferring them to other similar tasks. Grade 3 students successfully transferred their new skills to new tasks, while grade 4 children were able to retain the skills for longer, doing better than untrained children of same age on pencil and paper tests 7 months later. What factors might account for this progression? From the perspective of Kuhn et al. (2000) we can hypothesise that the younger children do not yet have the mental models of causality that would prompt them to see the necessity for using CVS strategies consistently. However, the studies reported next suggest a complex mix of contributing factors. It seems to us that this research has immediate potential to inform good teaching practice.

Schauble (1996) and her team compared the investigative skills of 10 children, with an average age of 11, with 10 adults who had had no formal science training. Both groups carried out 2 series of investigations across several weeks, and the researchers tracked the development of their skills as they went along. Thus, this was a microgenetic developmental study, designed to track the actual development of each individual across the course of the intervention. One task involved determining the causal variables for patterns of boat movement in a model canal. Some variables had counter-intuitive effects and some interacted with each other, complicating the causal patterns to be unravelled. The second task involved the suspension of objects in water at different depths, using a spring. This task had a similar level of variable complexity to the canal task. In part of a different research programme, Toth, Klahr, and Chen (2000) took a complimentary focus. They investigated children’s ability to learn to create their own CVS investigations and to evaluate CVS investigations designed by others. The researchers used carefully structured instruction strategies that had been informed by the earlier research of Chen and Klahr (1999). The practical implications of this work will be reported in Section Six. The areas of congruence between the reported findings from these 2 research programmes are outlined next.

Schauble (1996) and her colleagues found that the children in their study experienced varying degrees of difficulty in making valid inferences about certain types of variables. They identify single causal variables (inferences of inclusion) as the easiest to master. Inclusion episodes involve “fair” (unconfounded CVS) tests in contexts that allow children to confirm their own theories with the evidence they generate. Support for this argument is provided by the work of Chin and Malhotra (2002), which we outline in the next sub-section. Toth et al. (2000) similarly found that children can identify and use simple unconfounded CVS tests more easily than other types in the absence of formal instruction.

We saw episodes during the NEMP task analysis where the agreement between the unfolding events and the children’s ideas about what they thought should happen encouraged them and gave them confidence that they were working correctly.

Schauble (1996) reports that non-causal variables (inferences of exclusion) are somewhat harder to master because they require children to integrate information across several trials, comparing the effects of controlling different variables as they go. Similarly Toth et al. found that non-contrastive investigations (where children had to identify an irrelevant variable) were not quite as easy for them to recognise, or to learn to produce with appropriate instruction. It seems to us that the possibility of exclusion is unlikely to even occur to children until they hold at least an emergent analysis model on Kuhn’s mental models progression, and so we have aligned these ideas in the framework clusters we have developed.

Indeterminate CVS tests – those that require recognition that evidence does not exist to support a resolved conclusion – are also more difficult for both children and adults to recognise (Schauble, 1996). Similarly again, Toth et al. found that single and multiply confounded CVS tests are the hardest for children to identify – and that, following formal instruction, children did not show as much improvement in evaluating these types of investigations as they did with unconfounded and non-contrastive investigations. By definition, confounded CVS tests will obviously generate indeterminate data, although indeterminacy can also be linked to more complex considerations of theory/evidence links, as explored below. Nevertheless, it seemed to us that these findings align logically with Smith et al.’s (2000) criteria concerning ability to see inconsistencies in peers/personal thinking, and also with the development of a more interactive-analysis mental model from Kuhn et al.’s (2000) work. Thus, while Schauble does not differentiate degrees of difficulty between exclusion and indeterminacy, we chose to place these in clusters 4 and 5 respectively in our evolving framework.

Progression in planning
Schauble (1996) reports that adults were typically more systematic than children when working through sequences of trials. Her team identified 4 patterns of increasing sophistication in systematic planning and carrying out.

At the lowest level there was no evidence of a plan or system. Children working in this manner would typically draw conclusions from single tests, or sometimes make post-hoc comparisons with previous tests. This clearly aligns with the meta-level understanding of each investigation as a separate episode, already identified as a feature of cluster 1. Schauble next introduces the term local chaining (p. 109) to describe emergent attempts at being more systematic. Children who worked in this way focused on pairs of trials, without relating these to a larger plan structure, and this could lead them to repeat trials they had already carried out without recognising that they had done so. This seems to us to represent an emergent recognition of the need to explain investigations in terms of more than one episode, and so we have placed this idea in cluster 2.

Some children did develop a simple plan and initially used a VOTAT – vary one thing at a time – strategy. However, after 5 or more such trials they “lost their place” (Schauble, 1996, p. 109) in the face of the accumulating body of evidence, and so the initial plan was abandoned or forgotten. This finding resonates with reports from the longitudinal study of German primary school children (Bullock and Ziegler, 1999). The German researchers checked for differences between children who could recognise, but not produce, controlled experiments at age 12 and those who could consistently both recognise and produce simple CVS tests. The 2 most important differences they found were having access to explicit verbal knowledge about experimental control and memory span. We have used the juxtaposition of these 2 quite different studies to link the ability to plan and carry out sequences of investigations with increasing memory capacity in cluster 3 of the evolving framework.

Schauble (1996) reports that some participants had the ability to produce a “global plan” that “reflected the overall structure of the experimental space” (p. 109). Adults were more likely than children to review such a plan as they proceeded through a series of trials. A plan that can anticipate a whole sequence of trials obviously places demands on the memory. Some researchers have reported success with using “representational scaffolding” in the form of tables, charts, and computer mapping programs, to help children develop a more global view of the whole experimental space (Toth, Suthers, and Lesgold, 2002). Similarly, the researchers in the German longitudinal study found that a simple training intervention that “fostered representation of the entire problem space” (p. 51) made a “dramatic difference” to the ability of 11-year-old children to produce unconfounded CVS tests (Bullock and Ziegler, 1999). In the absence of such scaffolding, the ability to plan globally presupposes a meta-representational awareness of the possibility of relationships between combinations of variables – that is, an interactive-analysis mental model (Kuhn et al., 2000). Thus we tentatively placed the emergent use of global planning in the fourth cluster, and its consistent use in cluster 5 of the evolving framework.

Support for this decision came from the findings of research that investigated the causal reasoning of a group of community college students, with an explicit focus on how they actually reasoned about interactions between variables (Zohar, 1995). Noting that the more usual focus on single variable CVS strategies neglects instances of co-variation between variables, this research team hypothesised that strategic competence in producing CVS tests is a “necessary but insufficient” (p. 1040), condition for carrying out an effective inquiry. They designed 4 “microworld” investigations with different contexts but similar structures. In each of these microworlds 2 variables were non-causal, 1 had a simple causal effect, 1 had a causal effect only when in interaction with one specific level of other causal variable, and one 3-level variable had a partial, curvi-linear effect. This complexity meant that it was possible to run pairs of CVS tests that, when considered in isolation, appeared to generate conflicting evidence. To illustrate, one task that was adapted from the earlier research of Scauble involved determining the factors that influenced boat speed on a canal. If weight and boat size are considered as the focus variables, the 4 CVS tests that should be carried out are: small boat with weight/small boat without weight; and large boat with weight/large boat without weight. However, in the microworld designed:

The two conclusions described here contradict each other; neither of these two sets of experiments considered separately provides a full explanation of the phenomenon under investigation. To resolve this contradiction, a broader picture must be drawn: A second-order investigation needs to be carried out to discover the interactive effect of weight and boat size. To make the interactive inference that the causal effect of weight depends on the size of the boat and that it makes a difference in a small boat but not in large boat, the investigation requires the full set of four experiments. Only such a double set of comparisons may lead to an interaction inference (Zohar, 1995, p. 1046).

Thus, controlling variables in simple CVS tests is a necessary but insufficient investigative strategy in this type of situation. Zohar goes on to compare the stumbling confusion of some of the lay participants with the orderly manner in which two “expert” investigators devised meta-strategic plans that allowed them to detect the interactions relatively quickly. These findings clearly align the unprompted use of global planning with a well-developed “interactive analysis” mental model. The use of lay adults in this study is a timely reminder that the fifth cluster of the developmental framework we have devised may never be reached in the absence of opportunities to build a sophisticated metacognitive awareness of investigative strategies. The provision of appropriately structured and supported learning experiences is a huge challenge for teachers and for those who are teacher educators.

ATTENDING TO THEORY/EVIDENCE LINKS
Most of the “fair testing” research reported above has focused on what Klahr (1999) calls the “experiment space” of the investigative process. He points out that there are actually 3 major interdependent processes in scientific discovery, although very few studies of children’s investigative skills actually attend to all 3. The other 2 are the “hypothesis space”, and “evidence evaluation”. Each of the 3 sets of processes can be further subdivided into domain specific and domain general cells, depending on whether the knowledge being drawn on is specific to the focus investigation or more general.

The literature reported here was originally intended to inform our observations of children’s skills as we observed these on the NEMP tapes, and to assist us with our analysis of the fit between these observations and the Exemplars Matrix. Each of the 3 NEMP tasks began with a “ready made” investigative situation, in which children were free only to decide on the details of how they would manage a CVS strategy. Although some “planning” was required of the children, this does not constitute thinking in the “hypothesis space”, which would have required the children to decide on the parameters of the investigative situation, grounding their planning decisions in their previous thinking, experiences, and questions. Similarly, evaluation implies a discussion of whether or not these initial ideas were supported by the evidence produced, thereby linking evaluation back to purposes. Without the hypothesis space, the evaluation space may also remain meaningless.

As reported in Section Three, many NEMP groups had scant understanding of the purposes of the 3 tasks beyond the most obvious requirement for task completion, and their “discussion” was accordingly very brief. In some cases the teacher seemed not to have a sense of theory/evidence links either, and the discussion was inevitably superficial, or truncated by haste to move the children to the next task. Despite the lack of overt reference to theory in the tasks we observed, in this sub-section we do make some links between the research we report and the patterns we observed because of a subtle but important shift in focus. As this sub-section unfolded it became increasingly apparent that questions of progression in children’s knowledge and skills cannot be separated from considerations of progression in the selection and structuring of the contexts of the investigative tasks. While the role of contexts in determining progression has not been the direct focus of the research we discuss, some issues that emerge seem to provide very useful guidance for teachers.

Children’s access to an expanding knowledge base
In their longitudinal study of the development of children’s investigative skills, Bullock and Ziegler, (1999) found that about 42 percent of all linear growth in individual children was explained by just 2 variables – logical reasoning and general knowledge. Presumably, children with a broad general knowledge can envisage more types of episodes in which to ground their cause/effect inferences. Reflecting on the role of “domain specific” knowledge in making personal sense of investigative experiences, Schauble comments that:

There are notable differences in the “libraries” of causal mechanisms cited by children and adults, with adults more likely to propose mechanisms that appropriately applied to the situation and that accounted for the observable data. Even when children and adults had similar concepts, they did not necessarily access them with the same facility in the context of these tasks. Participants' attempts to reason about these knowledge-rich systems thus suggest that the contribution of prior knowledge to scientific reasoning may be deeper and more domain specific than most “experimentation strategy” studies have acknowledged (Schauble, 1996, pp. 117–118).

Libraries of causal events are prior knowledge that is not “general knowledge” in the usual sense, although we have suggested that the two are likely to be interconnected. Based on the research of Smith et al. (2000) we have already indicated the importance of gaining an expanding repertoire of “scientific” ideas in the “personal knowledge skills” aspect of the evolving framework. Clearly, children need to experience a range of rich exploratory contexts to develop this specific type of “general knowledge”. We note here that this was also recommended as one finding of the recent literature review of effective pedagogy to raise achievement in science learning (Hipkins et al., 2002).

The development of observation/theory links
The research of Chinn and Malhotra (2002) provides a more detailed analysis of the links between observations children make during investigations, the ideas they bring to these observations, and the learning that they achieve. In an attempt to better describe the cognitive complexities of conceptual change Chinn and Malhotra investigated children’s responses to anomalous data during 4 sets of experimental interventions. They designed deceptively simple investigations where the empirical evidence that addressed the question posed could easily seem ambiguous against a “noisy” background (as, for example, determining whether 2 objects of different mass hit the ground at different times if they are dropped at the same time from the same height).

Chinn and Malhotra found what they called an “asymmetrical bias” in children’s observations. Those who initially made correct predictions were highly likely to observe accurately. On the other hand, children whose initial predictions were incorrect did not necessarily make matching incorrect observations. Accordingly, Chinn and Malhotra suggest that children’s observations are “schema facilitated and not schema determined” (p. 332). Knowing what to look for can help children observe accurately, regardless of the “noise” in a potentially anomalous situation. They further demonstrated that where children were given opportunities to make predictions explicitly based on correct explanations that were provided to them8, their observations were likely to be correct and to prompt conceptual change:

Conceptual change is impeded largely at observation, and observations are accurate only when children can apply a perceptual schema that helps them detect the outcome of an experiment against a noisy background. Explanations operated by providing students with schema that they could use to guide observations in an ambiguous-stimulus environment (Chinn and Malhotra, 2002, p. 338).

These findings again support the assertion that evidence that disconfirms personal theories is more difficult for children to process than that which confirms them. However, Chinn and Malhotra also alert us to the critical importance of context. As part of their decision making to take account of the “readiness” of children, teachers could consider the selection of contexts that can allow the observations that children will be required to make to be “cued” to align with the explanatory theories they are likely to find plausible. Much advice is given about the latter aspect of this combination (i.e. potential progression in children’s theory development) in traditional curricula, including SNZC. We instead turn our attention to the structuring of inquiry contexts in ways that might assist teachers in matching observation tasks to children’s stage of skills development.

Awareness of data patterns
Toth, Khlar, and Chen (2000) identified an interesting type of response of “know-all-along students” to the explicit teaching of fair testing skills. These children were already able to consistently produce CVS tests before instruction, and they continued to do so after instruction. However, they became less certain of the justifications they made for the strategies they used after CVS instruction, even as they continued to generate unconfounded CVS tests. The researchers suggest that these children were becoming more attentive to variation in data outcomes, and that this had raised their awareness of potential sources of experimental error, thus rendering them less certain of the justifications they gave for the tests they had run.

Might Bullock and Zeiger’s finding that memory capacity limits children’s ability to conceptualise the whole experimental space help explain this finding? Perhaps attention turns to more subtle features of an investigation only once memory space is freed from a laborious focus on the CVS design and implementation? Certainly it seemed to us that many of the children we observed on the NEMP tapes saw each separate test as a stand-alone event. Their laborious measuring and recording of each result seems to us to have made it unlikely they carried an awareness that there even could be an overall pattern of data generated. Some attention was given to the broadest of such possible patterns in the limited discussion at the end of each investigation, but we think some specific memory aiding strategies could easily be implemented to help make patterns of data variation much more visible to young children.

Probing children’s understanding of error in experimental data gathering (Masnick and Klahr, (2001) point out that error is less important when the goal is to compare a relative measure of two situations than when it is to measure absolute data. They note that children can more confidently predict and justify overall trends when results are categoric than when data are continuous. In their study, even grade 2 children could describe likely sources of variation in trials that involved relative rather than absolute measurements. Masnick and Klahr suggest that children have a “nascent understanding” that main effects should be robust, even when there is variability in individual samples. These insights seem to us to hold considerable promise for helping teachers shape contexts in specific ways that support the development of children’s investigative skills, especially at the earlier stages of progression. Accordingly, we have used the criterion of collecting categoric rather than continuous data to differentiate early attempts at producing fair tests (cluster two) from later stages of progression. Once continuous data are introduced, it also seems that careful consideration of the contexts in which measurements are to be made could assist in helping children develop awareness of data variation as a key observational skill, as outlined next.

A juxtaposition of our observations of children working on the NEMP tasks with Schauble’s (1996) rich descriptions of her participants’ investigations has helped us to specify some contextual features that contribute to the observational challenge of measurements to be made:

• Categoric or continuous data – counting/comparing is easier than measuring to a scale and describing as a number pattern;
• Familiarity with the measuring instrument, and the scale(s) it provides – instruments with multiple scales and/or fine gradations require intense concentration of children and so are likely to separate the investigation into a series of seemingly disconnected events;
• Time available to determine the measurement – a stationary object can be measured at leisure, a moving one must be “stopped” in the appropriate instant, a sequence without a single clear finishing time requires knowledge of research protocols for specifying an endpoint;
• Horizontal or vertical scale to be read — parallax is more likely to be an issue with a vertical scale, as in the Ball Bounce task;
• The magnitude of the difference to be observed (effect size) – this impacts on the “obviousness” of the evidence and, as outlined below, can invoke “theory saving” beliefs when differences are small enough to be discounted as errors.

These contextual considerations could be used to better match an investigative task to the level of progression of children’s investigative skills. We illustrate how this might have been done with respect to each of the selected NEMP tasks in Section Six of the report. Meeting several of these types of challenges within one investigation should arguably be postponed until students are able to consistently produce unconfounded CVS tests. Accordingly, we have identified these skills as cluster four attributes.

Awareness of experimental error
Both the 1995 and 1999 NEMP science reports commented on children’s failure to plan and carry out repetition of individual tests (Crooks and Flockton, 1996; 2000). The research discussed above has led us to question whether this emphasis, implicitly grounded as it is in protocols to manage experimental error, is developmentally appropriate for young children. Might a focus on simple awareness of variations in data patterns be more productive for children whose investigative skills are still in the early stages of development? The research reported next led us to align the management of experimental error with cluster five of our evolving framework.

Rollnick, Lubben, Lotz, and Dlamini (2002) identified a progression in meta-strategic awareness of the necessity to manage measurement errors amongst undergraduate chemistry students. They describe a “point” paradigm in which each separate measurement made is seen as independent of all others that are made and so each individual measurement could potentially represent the “true” measurement of the situation, if sufficient care was taken. We certainly saw evidence of this sort of thinking during the tape reanalysis. (“Measure really, really carefully.”) Contrasting with this is the more sophisticated “set” paradigm in which individual measurements are seen as approximations of the true value and awareness of variation encompasses ideas such as the spread of data. In this “set” view a number of measurements must be combined and characterised by mathematical operations such as the calculation of the mean and standard deviation for an actual value to be accurately described. Significantly, Rollnick et al. (2002) describe an intermediate stage at which students use “set” actions but “point” reasoning. The researchers suggest these students are merely following an algorithmic process that has been inculcated during their previous education. They describe this as unhelpful and “an impediment to moving learners towards a set paradigm in much the same way that alternative conceptions about concepts impede learning of scientific concepts” (p.3).

In light of their experiences with 2 different groups of students, Rollnick et al. recommend that “in order to become consistent users of a set paradigm, students need to have authentic experiences of data handling where the goal is a finding that does not necessarily correspond to a correct answer in a demonstrator’s marking memorandum” (p. 17). While this could be read as a negative comment about certain university assessment contexts, it also seems to imply that such experiences should allow students to consciously explore data patterns that emerge in a specific investigative context. If such a focus is to begin from a younger age, as we have advocated above, teachers should be supported to choose contexts where data variations can be both observed and documented at the appropriate investigative skill levels. We return to this challenge in Section Six.

Different types of scientific investigations draw on differing research protocols as part of their anticipatory management of known types of experimental error. Here, too, context could play an important role in determining progression in awareness of patterns in data variation. Haigh (1999), commenting on Year 12 students' ability to carry out open investigations in biology, notes that sound knowledge of CVS strategies is a necessary but not sufficient basis for managing data variation:

Although these students’ written work indicated that they knew about the principles of fair testing they did not always demonstrate consistent application of these principles. When planning and gathering data these students had a poor understanding of experimental protocols relating to sample size and replication. They had difficulty identifying and manipulating variables and did not always specify measurements with sufficient precision (Haigh, 1999, p. 7).

Clearly, the management of experimental error in all its various potential manifestations presents a complex set of challenges whose specifics are unique to each type of authentic investigation. However, we have also suggested that it is possible to simplify data gathering procedures without compromising children’s growing awareness of these issues, and that manipulation of the context of the investigation might be one aspect of actively teaching for progression.

Issues of “data distortion” and “theory saving”
Schauble (1996) describes some ways in which her research participants’ personal theories of cause and effect seemed to influence the manner in which data were collected and then either accepted or discounted by both children and adults. She illustrates a process that she calls “data distortion” as follows:

…when participants measured the spring length with the ruler, they could raise or lower their line of sight, resulting in slight fluctuations of the observed value. Similarly, participants could produce variability with the stopwatch used to measure travel time in the canal task. Beyond the difficulties naturally associated with timing events to the nearest hundredths of a second, there were opportunities for intentional delays or “jumping the gun” (Schauble, 1996, p. 114).

Schauble is not suggesting here that her participants deliberately cheated – rather that data distortion during measurement is one way in which they subconsciously attempted to align their prior ideas of cause and effect with the observations they made. In an attempt to avoid this data distortion effect, Zohar’s (1995) team simplified Schauble’s boat task so that only relative speed need be observed. They did this by using coloured flags on the side of the canal. Participants stated how many flags a boat passed on each test run rather than measuring the actual distance travelled. With the earlier source of potential error thus removed, Zohar’s team detected a process they called “theory saving” that operated at a later stage of the investigation. When pairs of CVS tests yielded seemingly conflicting results, some participants made limited inferences, accepting only the inference drawn from the paired CVS tests that agreed with their prior causal thinking. For example, if they had a prior belief that weight does make a difference to boat speed, they accepted the evidence generated by the small boat/weight and small boat/no weight pair of tests. However, the seemingly conflicting inference provided by the equivalent test pair with the larger boats was simply ignored when the findings were reported. Obviously, participants who used theory saving strategies were unable to use their investigations to detect and describe the interactive effects of some of the variables.

Some important NOS issues are captured in the theory/evidence interactions described by these researchers. Schauble points out that scientists must also wrestle with the process of drawing correct inferences from their empirical evidence:

Phenomena like measurement error and data distortion underline the fact that theories and data are inextricably intertwined. Theory guides fundamental decisions such as which independent variables should be considered as potential causes ….With the hindsight provided by a scientifically accepted model, researchers can conceptually separate theory and data in an experimentation task, but for the scientist laboring before the critical conceptualisation is made, or for the experimental participant who does not already understand the problem domain, such distinctions are unavailable (Schauble, 1996, p. 115).

Like Zohar’s “expert” investigators, scientists must proceed from an explicit understanding that evidence may be explained in more than one way, and that testing to eliminate alternative hypotheses is an essential feature of scientific inquiry. We have aligned this aspect of the “view of scientists goals/methods” (see page 62) with the interactive analysis mental model in cluster five of the evolving framework. Both are linked to the availability of coherent overarching explanatory frameworks of science knowledge in the “personal knowledge skills” aspect, and to specific types of personal investigative skills. We reiterate that many school students, and possibly some undergraduate students, will not reach this level, at least with the sorts of investigative experiences to which they are typically exposed at present.

We have already noted the likelihood of strong links between personal theories and the inferences children draw from the evidence generated by their investigations. Absolute measurements inevitably generate measurement errors and Schauble (1996) has noted that children and adults have difficulty in distinguishing variation caused by measurement errors from variation due to true differences between the experimental conditions. In her investigations, when in doubt both children and adults fell back on their prior theories. If they expected a variable to have an effect, they interpreted small variations in measurements as a positive effect. If they did not expect an effect, they were more likely to interpret small variations as error. Here, as in previous sub-sections, the nature of children’s theory/evidence links may well form an important aspect of progression.

8. The researchers caution against using this finding to justify “teaching as telling”. Their explanations were provided in the context of a discussion grounded in children’s own thinking.

prev page / next page