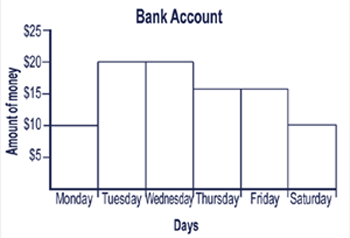
For this task, students were shown a graph of the amount of money in a bank account on six consecutive days. The instructions for what the teacher administrator was to say and do for this problem were as follows. Instructions of what to do are given in bold.

The final request to 'tell me a story…' asks for a personal response and for a story. The statement, 'Tell me a story to explain what is happening with the money' was not heard by some students as a request to explain deposits and withdrawals, but merely the amount of money in the account each day. There was no request for the mathematics to be foremost, or for mathematical language to be used. This disguised request for an explanation of a mathematical representation complicates the need to display understanding of the mathematics presented in the graph as students are expected to cross between modalities, from the modality of mathematics to that of providing a story that matches the graph.

A story that included reference to putting money in and taking money out so that there was more or less the following day as shown by the next bar would include the expected elements. However, conversational stories rarely include all of these elements. They are often elliptical, expecting the listener to understand that if you took money out of course the graph would show a lower level the next day. In formal mathematical expression, the causal connectives are essential.

In this chapter we first discuss the accuracy, type of stories told, and linguistic features by age group. Then we present a section on the explanatory text structures used. This is followed by an analysis of the hesitancies in the students' language.

Some of the Year 4 students took the request to tell a story literally and told elaborate stories, although these were not always stories of increases and decreases in a bank account. It appeared that when they gave only a description of the graph, the interviewers prompted them further for a story. Few stories reflected experience with a bank balance that changed daily. Stories were of several types, some stories being of more than one type. Some of these stories could be considered to be reflective of the students' backgrounds or their interest in stories from books or the news. Several associated the graph with only deposits or only withdrawals. In one case, this was a story of money being raised. This may have come from experience with school or church fund-raising where the amount raised daily had been displayed. These stories could be appropriate had the table been labelled 'Amount deposited in (deducted from) a bank account', rather than the amount the person 'has'. The appropriateness or inappropriateness of an answer depends on understanding of one word from the interviewer. This may not be enough of a clue to override the students' personal experience. These stories are discussed further in Chapter 7.

Table 6.1 gives the type of story told by each group of students. By the criteria expected for the test, only the first column would be considered correct. The totals for each group may be greater than six if one type of story was given and then they were pressed by the teacher administrator.

Thus 13 of the 36 students did not give the type of story that was expected. All of these were lower decile students. Nine of these were Pacific and four were non-Pacific students. These differences between economic groups were highly significant (p=0.00029)

Seven students did as the question expected and made up a story to explain the change of the graph. Sixteen students simply reported what had happened on the graph with no causal statement. This response was most common among the high decile students and least common among the Pacific, low decile students. This suggests that students who were mostly of the same ethnic group as the interviewers believed that the mathematics of graph reading was what was important, not the story.

There were marked differences in the type of stories told by these Year 4 students. Three of 12 Year 4 Pasifika boys from low decile schools mentioned robbers or stealing in their stories as did one Year 4, high decile girl. Stories of lower decile children included 'they borrowed it because they had no money, they needed it to buy food, to buy lunch for their daughter, for school' (Pasifika girl); 'mum hates going to the bank' (Pasifika boy), 'when my dad gets paid, yeah, he'll put money in the bank for me'(Pasifika boy) and money owned by 'the people' (non-Pasifika boy, Pasifika boy).

Three Year 4 boys from high decile schools talked of the money going up and down, possibly treating it like the share market or possibly just referring to the graph, thus ignoring the story shell expected by the final question. They commented that the graph went up or down but did not attribute an external agent to these changes. An example of this was:

Well, the money, on Monday it is, it was on ten dollars, then on Tuesday it grew (unintel) it went to twenty dollars, and on Wednesday it's still on twenty dollars, then Thursday it lowered down, and it was (pause) on fifteen dollars, then on Friday it was fifteen dollars again and on Saturday it was on ten dollars.

Two high decile girls treated it like an exercise in story telling. One started her story 'Once there was a little boy named James and he had lots of money…'. The other included specific purchases made, as in 'he went to the store and bought some sugar and some cherries'. These story telling skills are similar to those encouraged in school, where emphasis is placed on writing and editing good stories as an aspect of literacy. For these girls, the story telling aspect seems to have been more important than the mathematics in the representation.

The agents in the stories told were other people, not the student. One girl from a high decile school asked 'how do I know if it is a man or a girl?' This was one indication that most students did not see bank accounts as something that they owned or looked at regularly. When 'I' was used it was usually in conversation, as in 'I don't know', or 'I mean'. Within the explanatory story, only one child used 'I' as the agent of her story, and this was a modification of a clause that started 'Monday we had, I had ten dollars'. Agents were usually the same throughout a story, although a story might use 'the people' initially and then 'they' for later references to the person. Counting only the main agent in a story, 'they' was most common (8) followed by 'he' (4). Other agents used were: the person: 2; the people: 2; someone: 3; robber 2; my dad, the man, and she.

For the students who reported on the characteristics of the graph, bars or amounts of money were referred to as 'it'. This occurred in 11 cases, sometimes in conjunction with the personal agents listed above.

Many of the verbs used were specific to money (19%). These included 'put in', 'stole', 'saved', 'spent', 'borrowed', 'costed' [sic], 'earns' and 'gets paid'. All of these would be specific to the context and inappropriate for an identical graph that was, for example, of rainfall. They indicate that students were attending to the story context that was given to them. Some of these verbs, like 'spent' were consistent with the mathematical comparisons required while others were not.

More common were verbs that referred directly to the comparison of the height of columns (26%). Some of these were not strictly comparative. These included 'grew', 'went up'. Others might be considered transitional to mathematical expressions, like 'goes bigger' and 'goes smaller'. Others, all used by one student, refer more conventionally to mathematical comparison. These were 'is shortest', 'is in the middle', 'is highest', 'is the same' (Pasifika boy from low decile school).

Other verbs were non-mathematical, with the largest proportion being static (36%). There was only one example of a mathematical verb. This was 'makes', used to mean equals (Pasifika boy from low decile school).

As stated above, in a story about this graph one would have expected to hear some causal connectives such as 'the next day there was the same amount of money because he didn't add any or take any out'

In fact few Year 4 students used causal connectives. Only 14% of the connectives were causal, primarily either 'because' or 'so'. These were used by nine students, spread across five subgroups. They were used by both boys and girls of all three main subgroups. These students rarely used more than one or two causal connectives.

The largest proportion of connectives (84%) was additive ones, connecting the stories for each column in the graph or part of the story. These connectives were 'and' (54%), 'then' (12%), and 'and then' (20%). Other connectives used, in small numbers, were 'but' and 'when' (1% each). The discrepancy between causal and additive connectives was found in every group of students. There was little correlation between the length of story told and the variety of connectives used. For example, the high decile girls, all told extended stories that had episodes connected by 'and'. Only one of these students used the causal 'so'.

Only five of the 36 students did not describe both the increases and decreases on the graph or give an explanation involving both putting money in and taking it out. As was the case for the Year 4 students, all of these were low decile students. This difference between high and low decile students was significant (p = 0.01031).

Year 8 students were significantly better at giving an appropriate answer - either a story closely tied to the graph or a mathematical description of the graph ¬- than were the Year 4 students, at the 0.05 level (p = 0.01717).

There were instances in these interviews, as in those for the Year 4 students, where teacher administrators prodded for more of a story when students only gave what happened on the graph.

There was far less difference in the type of stories told by these older students than by Year 4 students, indicating that these students had a clearer idea of what was expected of them, and a better idea of what happened in bank accounts. There was no obvious difference in the type of stories told by students from different ethnic or economic backgrounds.

When the Year 8 students told stories, they were more closely allied to what might have happened in a bank account than were those of the Year 4 students. For example,

He's ah just got his bank account and he got ten dollars with it, his um mum put in another ten dollars and he's got twenty dollars, but he ah, didn't do all the jobs in his house so um, and he wanted to buy something, he didn't get his pocket money for not doing the jobs in the house so he took some out of his money, and ah he left the his bank account alone for another day, and then he decided he'd that he um, wanted something else which was better than the last one and so he got out some more money.(non-Pasifika boy)

There was one instance of a non-Pasifika girl from a low decile school starting her story with a story-telling convention. This was 'Well, one day Fred…' There was also one instance of a student asking the interviewer, 'Do I have to tell who they are?' (low decile, non-Pasifika girl). This is similar to the Year 4 student who asked 'how do I know if it is a man or a girl?'(girl from high decile school). There were no instances of robbers or of personal stories that reflected the students' families' experience with banks. The instances of stories telling only how much was added or how much was taken out might be accurate, if the graph had been labelled 'Amount deposited in (deducted from) a bank account daily', as would those of the Year 4 students.

The agents of students' stories were other people, as they were for Year 4 students, or the columns on the graph. Instances of the use of 'I' were related to personal, conversational statements like 'what should I say?'. There was one instance of 'I' as the agent within the story-telling conventions where a quotation was part of the story.

he, um, actually um, had ten dollars in the, bank account and, he thought oh, he got, he got his next allowance or pocket money or something, and then like, so, thought well I should deposit ten dollars, (Year 8 boy from high decile school).

All students who gave explanations used a name or pronoun for the person in the story (usually he or they); a pronoun referring to the graph (usually 'it') or an existential agent, as … 'on Monday there was ten dollars…' (Year 8 non-PI boy). When the main agent used by a particular student was analysed, 25 students used 'he', 'she', 'they' or people as agent; 9 used 'it', the day of the week, or an existential 'there' referring to the column height; and 2 did not include an agent in their answer. There was little difference between ethnic or economic groups or genders.

In comparison to the Year 4 students, more Year 8 students used causal connectives. In this age group 22% of all connectives were causal. Some students used a variety of causal and additive connectives. The following example includes this variety, and has the connectives in bold. ..

So like for each day or? [Q] Okay, okay...um .. m Monday the amount of money was ten dollars, Tuesday and Wednesday it were quite high, and there were twenty dollars, Thursday it wasn't not that great but better than Monday, and Saturday was the same amount as Monday. [Q]That Tuesday's and Wednesday's had the most amount of money in the bank account, and Saturday's and Monday's don't have that much money. [Q] Ah, because Monday's like the start of the week and probably from Sunday they probably spent money from their account and then spent some more money on Monday and since it's Saturday, Saturday's like a shopping day and um, they probably went shopping and bought quite a lot of stuff so they didn't have much money in their bank account, and they probably work on Tuesdays and Wednesdays more than they do on Mondays and Fridays. (Year 8 girl from high decile school)

Of the Year 8 students, 5 students from high decile schools, 5 non-Pacific students from low decile schools, and 1 Pacific student from a low decile school used causal connectives in their responses. 7 students from high decile schools used additive connectives only, as did 6 Pacific students from low decile schools. Ten Pacific students used only additive connectives. The significant difference here is between non-Pacific students, both high and low decile, and Pacific students (p = 0.00536). Logical connectives are also discussed in relationship to combinations of text elements in the next sections.

These tables suggest that the students most likely to be accurate and use clear language are Year 8 boys from high decile schools, but that the differences between genders and deciles are not strong. Students who used unclear language and were accurate came from all groups, although more came from low decile than from high decile schools. The students most likely to be wrong and have unclear or elliptical language were Year 4 students from low decile schools of either ethnicity.

Among the Year 8 students, girls of all groups were more likely to use clear language when they told a story just based on the graph changes than were boys, but boys were more likely to tell a clear story based on saving and spending than were girls. An example of a girl's story describing the graph alone was the following:

Umm ... on Monday they have ten dollars, Tuesday and Wednesday they have twenty dollars, Thursday and Friday they have fifteen dollars, and then on Saturday they go back to ten dollars.

An example of a story of save/spend from a boy from a high decile school was:

On Monday whoever had ten dollars, and then on Tuesday they could have got their pocket money or got paid or something, it went up to twenty dollars they didn't spend any money on Wednesday, then they spent .. oh, is it fif, sixteen .. it looks as if they spent four dollars, so they had sixteen dollars, then they didn't spend any money on Friday, and then they spent some money on Sun, Saturday, which means they had eleven dollars left, or ten, hold on .. yeah ten dollars.

Pacific boys from low decile schools were also likely to use clear language when either giving a save or spend story or when providing an add or deduct story. The following is an example of these types of stories.

On Monday they only have ten dollars, but on Tuesday it rises, and on Wednesday it still stays the same, then on Thursday, they probably spent a little and it went little, then on Friday stayed the same, and on Saturday it went back to ten dollars.

As can be seen from the last example, the type of story is not always easily categorised, with some containing elements of more than one kind. This last example is considered to be predominantly about the process of getting bigger or smaller but does mention spending as well as making oblique references to the graph, through the use of 'it'.

The types of Premises in the text structures were related strongly to the type of story. The text structures are discussed in more detail in the next sections.

The text elements that the students used in responding to this task were predominantly Premise and Consequence. However, like the Weigh Up task, there were examples of students using other elements such as Conclusions, Elaborators and Suppositions. The different elements are described in the next paragraphs.

Three students used Premises followed by an implicit Conclusion. Two were Pacific girls and the other was a boy from a high decile school. The Conclusions used were implicit: 'that's how much money they got … and that's all'; 'And the large money is twenty dollars .. second one is fif, six, seventeen and a half, that one is ten dollars, it's finished'; and '...Money's going um, it starts at ten and it's going up higher …. Hmm, that's all'. This final clause was added after a comment by the teacher administrator.

Different types of Premises were used in the responses. However, often a range of Premises was used making it difficult to code the responses definitively as was done with the responses to the Motorway task. The following example comes from a Year 4 student.

Um, there's ten dollars on Monday, twenty dollars on Tuesday and Wednesday, and fifteen dollars on Thursday and Friday .. and, ten dollars on Saturday. Q Um, ah, they might have only got ten dollars and then, then the next day they put another ten dollars onto it .. and then on, then on, then on Thursday, um, someone might have stole some of their money, and on, and .. and on Friday they didn't bring any money in, so then another bank robber came in and stole all their money again.

'There's ten dollars on Monday' was coded as a monetary Premise, as it was based on the money, while 'they might have only got ten dollars' was coded as a personal Premise, as it had a person (although unidentified) as the main actor in the clause. This next example comes from a Year 8 student:

...Umm, started off low and then going high and then going down again.
Q
Um, she's got a raise, and then she got dropped down again.

In the first sentence, all the clauses were coded as 'graphical' Premises, as they are all referring to the graph. However, after the teacher's comment or question, the next sentence contains two personal Premises.

Although the number of students who use this combination of elements was small, it was most commonly used by students from low decile schools, and not in Pacific communities. Interestingly, three students joined these clauses with 'because', one student used 'when', while the remaining two students did not use any logical connector.

As with the Weigh Up task, clauses which set up propositions were labelled as Suppositions. In two cases, 'say' was used by students to indicate that the specific example which followed was not necessarily exact. The first example of this came from a Year 8 girl at a low decile school who was not a Pacific Islander. At the end of her response she said, 'and then on Saturday it .. dropped .. to .. say about ..ten dollars.' In the other example 'say' was used to suggest that the series of actions outlined were hypothetical; '....Well, if this is the amount of money, and these are the days, say he came into the bank on Monday, and he like put ten dollars into his bank account then it shows that he's got ten dollars'. Suppositions were more common in the Weigh Up task and are discussed in more detail in that chapter.

The other element in this task was an Elaborator. Most often this was a relative clause which followed a verb to do with a mental action such as 'decide' or 'means', or a relative clause providing extra information about a previous clause or which was embedded within the main clause and provided extra information about an actor or an event. The following is an example from a Year 4 Pacific student attending a low decile school: 'the man that's stealing the money was come every week'. 'That's stealing the money' provides more information about 'the man'. Table 6.10 provides information about the use of Elaborators with Premises and Consequences.

There were eighteen students who used Elaborators with Premises, either embedded within or following immediately afterwards. Twelve of the eighteen students were girls, but there appeared to be no clear trends between any of the other groups. As well as elaborating Premises, they could also be found less commonly elaborating Consequences.

The following is an example from a Year 8 boy from a high decile school: 'he got his next allowance or pocket money or something, and then like, so, thought well I should deposit ten dollars', where 'well, I should deposit ten dollars' is an Elaborator of 'thought'. There were nine students who included an Elaborator with a consequence. Six of these were girls and six were from high decile schools. The following two tables provide information on the logical connectives which were used in the responses to this task. Given that many of the students doing this task gave a narrative either of someone adding or subtracting money from their bank account or told about the various features of the graph in a logical sequence, it could be predicted that there would be a variety of logical connectives used. This can be seen in the following example from a Year 8 student.

He's ah just got his bank account and he got ten dollars with it, his um mum put in another ten dollars and he's got twenty dollars, but he ah, didn't do all the jobs in his house so um, and he wanted to buy something, he didn't get his pocket money for not doing the jobs in the house so he took some out of his money, and ah he left the his bank account alone for another day, and then he decided he'd that he um, wanted something else which was better than the last one and so he got out some more money.

However, based on Grice's pragmatic maxim of orderliness, Peterson and McCabe (1991) suggested that 'the act of stating or describing one event before the other is automatically presumed to mean that the event mentioned first actually occurred first' (p. 34). The following tables, therefore, also provide information on the students who do not use a logical connective between a Premise and a Consequence or between two Premises.

As had occurred in the Motorway task, the use of logical connectives is fairly similar for the groups, with a few exceptions. More students from high decile schools used logical connectives and a larger range of them. They were also the group which chose most often not to use a logical connective between Premises. This suggests that while some students used more than one connective in their response, others chose not to use any at all.

However, there are differences in the use of some logical connectives in a Premise - Consequence combination and a Premise - Premise combination. 'So' as a causal connective is used more often to connect a Premise to a Consequence, but almost always by students from high decile schools and mostly by boys. The four students who used it to connect two Premises together were all in Year 4 and, also, mainly students from high decile schools. Peterson and McCabe (1991, p. 38), in reviewing the literature, suggested that 'narrators use connectives at transition points when they are departing from the timeline of their narratives to insert other relevant information, specifically so, but and occasionally because'. Below are the four extracts in which so is used to join two Premises together.

and on Friday they didn't bring any money in, so then another bank robber came in and stole all their money again (Year 4 non-Pacific boy from low decile school)

Q Five dollars, and they leave it there, for five dollars they spend, so they don't spend any money on Friday, and they spend five dollars more, so it makes ten dollars (Year 4 boy from a high decile school)

on Monday she had ten dollars, and um so on Tuesday and Wednesday she had the same amount, in twenty dollars (Year 4 girl from a high decile school)

on Monday the man, the man went to his bank account and, he had .. ten dollars in his bank account, so he, he, he left it to the next day to get some money out (Year 4 girl from a high decile school)

As can be seen from these extracts, none of the 'so's which connected two Premises seemed to fulfil this pragmatic role. The second extract suggests that the boy lost his thought pattern after a teacher utterance and the 'so' marks the point where he picks up the thread of what he is saying again. The other uses suggest that the speakers wanted the following Premises to be Consequences but have not made the connection sufficiently clear. McCabe and Peterson (1985), in research on the use of connectives by different ages of children, also found examples of 'so' where there were no causal links. Some of these were later explained, while others remained unexplained. They found no relationship to the age of speakers. On the other hand, Donaldson's (1986) research into children's use of connectives including 'so', found that logical causality was not mastered until the age of 8 and 9. Given that no similar examples were found amongst the Year 8 responses, it may be that part of the learning process for using 'so' effectively involves a period of time when it is used incorrectly. This would also explain the incorrect use of 'because' in the Better Buy task.

As well as logical connectives, the students used a range of other linguistic devices to suggest cohesion between ideas. One of these devices which was used by many students was the use of an adverb such as 'still' or 'again', or an adjective such as 'another', or 'same', which was used both as an adjective and as a noun. The following table outlines those who used these devices.

There are certainly significant differences between which groups using these devices. Only boys used 'still' and only girls used superlatives, such as 'shortest' and 'highest'. Students from high decile schools were more likely to use 'more' and comparatives, such as ' bigger' and 'lower', than students from low decile schools. Although the number of examples was small, it would seem that students from low decile schools were more likely to use superlatives than students from high decile schools.

Compared to the Better Buy task and to the Motorway task, where there were differences between the text structures, it is interesting to see that there are no trends for the different groups with this task. This could be partially because the text structures themselves were limited but maybe also because the students were uncertain about what was expected of them in this task. With limited variety in text structures and difficulty in determining what was an appropriate mathematical response, there seemed little point in looking at the text structures in comparison with appropriateness of response. Therefore, this section has not been provided in this chapter.