| Mathematical explanations and justifications have an important role in mathematics assessment (Bicknell, 1999). Yet, as was discussed in Chapter 1, it would seem that there is limited knowledge about what constitutes good examples of these. Part of the issue is knowing what the constituent parts of explanations and justifications are and how the differences between them are expressed. In this research, explanations were considered to be the description of what was done in solving a problem; and it had been expected that students would provide explanations when responding to the Weigh Up and Motorway task. Justifications were defined as the descriptions of why a certain strategy was adopted. The Better Buy and Bank Account tasks were expected to illicit justifications. Such a clear cut distinction was not found, especially when students struggled with the purpose of the task, as was the case with Bank Account. There was also a need to research the stages that students went through as they learnt how to produce a mathematical explanation or justification. Primary school children are not expected to produce mathematical proofs, which have been described as 'perhaps the ultimate in justifications' (Sowder & Harel, 1998, p. 670). Therefore, it was postulated that there might be series of linguistic features that students would need to learn as they progressed through school, so that, by the time they reached university they had mastered all of the features needed to construct a mathematical proof. It was anticipated that research on the responses from these tasks might contribute to understanding what these intermediate features might be. The differences found between groups in how they used these features would suggest that there is no clear pattern of mathematical language acquisition. Instead, what language is acquired and valued within certain situations is affected by a large number of issues. This chapter discusses in detail differences between text structures and the issues which seem to affect them, including the demographic characteristics of the students and the task requirements. First, it is worth reviewing what was already known about explanations and justifications. This research can be divided into what has been done at the macro or micro level of analysis. At the macro level, Krummheuer's (1995) work, based on the ideas of Toulmin (1969), on the components on mathematical arguments has been used by several other researchers, such as Yackel (2001) and Forman et al. (1998). These components were: claims, which were the suggested solutions; grounds, which were the unchallengeable facts from which the claims were developed; warrants, which were the information joining the grounds to the claims; and backings, which provided the constraints under which the warrants were valid. These researchers used these ideas to discover how students working together and with the teacher developed 'collective argumentation' (Forman et al., 1998). They were not looking so much at how individual students would produce explanations. Other macro level analysis was undertaken by Sowder and Harel (1998), which looked at high school and college students' responses and classified them according to the evidence used in them. These were: externally based proof schemes; empirical proof schemes; analytic proof schemes. However, this macro level research did not provide information on the linguistic structures which could be related to these components of arguments or types of justifications. The micro level research on students' explanations was that done by Bills (2002 and Bills & Grey, 2001). This research is considered micro level as it documented the linguistic features which seemed to be related to the accuracy of students' explanations as to 'what was in their head' (Bills, 2002, p. 100). Students who used 'I' or 'you' in a general sense, logical connectives such as 'because' and 'if' and present tense were more likely to give an accurate response. Typical classroom talk, such as using 'you', Bills (2002) hypothesised, was more likely to be used when students were successful. Certainly some of these linguistic features were evident in the responses to the four tasks, particularly the use of logical connectives and the use of personal pronouns. However, Bills did not relate these linguistic features to the different components of the explanations. By identifying the different text elements and the typical ways in which they were combined, we have been able to analyse the responses at both the macro and micro level. This builds on the work of Hasan (Halliday and Hasan,1985) who described how contextual configuration could be used to predict the text structure. As well, the reverse is also true, in that the text structure could be used to illuminate the contextual configuration. Hasan's (Halliday and Hasan, 1985) ideas about text structure require not only an identification of the different text elements, but also the recognition of what elements were compulsory, whether the positioning of elements were set and whether elements could be reiterated. This then allows for an investigation of linguistic features within the elements in order to attain a better understanding of these elements and how they are placed together to form the text structure. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aContextual configuration and text elements | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For all of the tasks, the contextual configuration was that students were in an interview situation at school with a teacher administrator who was asking questions to ascertain their mathematical knowledge. The particular knowledge being assessed was slightly different in all cases but all required the students to provide insights on how they perceived the mathematical relationship between objects, mathematical or physical (numerical and quantitative comparisons). It was therefore possible to see how the similarities in the text elements used across tasks was related to the general situation in which the student was operating. By looking at the differences between the responses for the tasks, it was possible to see how the task specifications as part of the contextual configuration influenced the text structures. It was quite clear that no elements were used by every student in every task. However, there were several elements which were used by many students in more than one task. Their use across tasks suggested that they were likely to be the text elements used consistently by students in responding to any mathematical assessment task orally. These elements were Premise, Consequence, Conclusion, Elaborator and Supposition. Table 8.1 shows the number out of a total of 431 students who used each of these text elements. In this table, the three sections of Weigh Up are considered different tasks, but there were only 71 samples for the Explanation section of the Weigh Up task. As the samples for the two 1997 tasks were of students from low, middle and high decile schools and the two 2001 tasks had students from only low and high decile schools there are problems in combining these results. In order to give an overview of which elements were used most often, the two groups of students, Pacific and non-Pacific, were totalled together and this amount then halved. No amounts were recorded for students from middle decile schools, and so amounts in the low and high decile columns do not add up to the total amounts. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.1. Use of text elements by different groups. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This table clearly shows that Premises were the most common text element used, with Introductions being the least common. There were few differences between groups using these elements. However, it would appear that girls use Suppositions and Elaborators more often than boys. It would also seem that Year 8 students tended to use more elements than Year 4 students, although the amount of difference varies for the different elements. Year 8 students used more Consequences, Conclusions, Suppositions and Elaborators. Students from high decile schools also used more Consequences, Conclusions and Elaborators than their peers at low decile schools. Within many of these elements, there were variations. The next sections look at each of these elements and their variations, before looking at how they were combined. The following sections show that very rarely did differences between groups persist across tasks, indicating that the tasks as part of the contextual configuration had a significant influence on the text structures. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aIntroduction | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This
element was used by only a few students in responding to four tasks.
These were Motorway and the Weigh Up Plan, Description and Explanation.
Introductions set the scene for a personalised or generalised response
to the task. Examples of these Introductions were 'I went' or 'you
could'. Given that most of the scripts for the tasks have the teacher
administrators saying 'Tell me how' or 'Explain to me,' it is, perhaps,
more surprising to find that so few students began their responses
by acknowledging such a request with an Introduction. It would seem
that in some tasks a Premise - Elaborator combination was used by
many students to fulfil the same purpose. An example of this combination
would be 'You'd tell them to use one of these' which was said by
a Year 4 student in responding to the Explanation section of the
Weigh Up task. Table 8.2 sets out who used Introductions. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.2. Use of Introductions in different tasks. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Even with such small numbers of students, there does not appear to be any distinction between the groups who used Introductions. Motorway was the only task where more than 10% of students used an Introduction. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aPremise | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In explanations and justifications, there is a need to provide evidence which would convince others (Sowder & Harel, 1998). The Premise is the linguistic embodiment of the basis for this evidence and, therefore, can be considered equivalent to Krummheuer's (1995) warrant. Certainly, as can be seen in Table 8.1, Premises were used by most students in most tasks, with little difference between groups. However, as can be seen by the reduced number of low decile students who used Premises in their responses to the Description part of the Weigh Up task, the task requirements have an effect even on this fundamental component. In these responses, Physical Consequences were used more often than Premises, as students had to describe their physical actions. These physical actions may have become the unspoken Premises. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.3. Use of Premises in different tasks. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Although Krummheuer (1995) suggested that warrants were unchallengeable facts, this was not the case with all Premises. Different types of Premises reflected the type of evidence which was given and can, therefore, be related to the proof schemes classified by Sowder and Harel (1998). In the responses to the Better Buy task, there were hypothetical or factual Premises. In the Motorway task responses, Premises were divided into factual, mathematical and personal. For the Bank Account task, there were personal, graphical or monetary Premises in the responses. In the Weigh Up task, there were no clear distinctions in the Premises which were used, as most students started their responses by relating an action that they would do or had done to one or more of the boxes. Factual Premises were in the responses to both the Better Buy and Motorway tasks and used information given in the question or in a resource. In the Better Buy task, factual Premises were more likely to be used in inaccurate responses. Students who gave them were less likely to combine them with Consequences and Conclusions to produce a train of reasoning. On the whole, it was more likely that students who gave factual Premises were girls, in Year 4 and attending low decile schools. Responses to the Motorway task showed a similar relationship as only four students followed a factual Premise with a Consequence whereas 13 students followed a mathematical Premise with a Consequence. This would suggest that students saw the most convincing evidence as deriving from an external source, as was also the case with the externally based proof schemes described by Sowder and Harel (1998). Only 4 out of the 20 students, who used a factual Premise, gave an accurate answer for this task. It seems that if students used this type of Premise, they were unlikely to develop them into a logical reason. In this task, the students who were most likely to give a factual Premise were Year 4 girls from low decile schools. There did not seem to be any differences in the ethnicity of the students who gave factual responses. As factual Premises used the unchallengeable facts, from those given in the question or in a resource used with the question, they could be considered grounds for a mathematical argument. However, as they were less likely to be used in an extended response, the links from them to their corresponding claims were too tenuous for clear mathematical explanations or justifications to be considered to have been given. This was the case for the Year 4 Pacific girl who gave factual Premises in the following response:
When the distribution of students in Better Buy and Motorway who used factual Premises is considered together, it would seem that Year 4 girls from low decile schools were most likely to use these Premises. Hypothetical Premises were the other type of Premise used in responses to the Better Buy task, but were more likely to be found in accurate responses. These Premises proposed an example as the basis for their justification and so could be classified as providing an empirical proof scheme (Sowder & Harel, 1998). They began with the logical connective 'if' and were most often followed by Consequences and then Conclusions, so that logical trains of thought were developed. Of the 25 students who used these Premises, 18 were in Year 8 but only 5 were from low decile schools. There did not appear to be any difference due to gender. In the Explanation section of the Weigh Up task, 25 students also began their Premise with 'if', suggesting a similarity with hypothetical Premises. Certainly, it would seem that in using 'if' students marked that an example was being proposed as an aid towards a general solution. It was interesting to note, however, that the differences between the groups found in the responses to the Better Buy task were not evident in the Weigh Up task. It is difficult to know whether this was due to only having a sample size of 72 for each task, or whether the context drawn upon for each task affected different groups' choice of linguistic features. Mathematical Premises in responses to the Motorway task were the only Premises to be given in accurate responses. However, unlike the hypothetical Premises, they did not have to be combined with a Consequence to be considered an accurate and clear response. For example, six Year 8 students, four from Pacific communities, were able to provide just a mathematical Premise and be considered correct. Given that students 133 are asked to 'Explain to me how you got your answer', providing a mathematical Premise such as 'Nine minutes times ninety-eight cars' is acceptable. It gives all the necessary information to answer the request appropriately. As mathematical Premises use mathematical calculations as their evidence for their solutions, they have similarities with factual Premises, as they draw on externally based proof schemes. Out of the 42 students who gave a mathematical Premise, 29 were Year 8 students. Although there would seem to be slightly fewer Pacific students who gave mathematical Premises (9 out of 42 students), there do not appear to be any gender or decile level of school attended differences for non-Pacific students. Mathematical and hypothetical Premises were mostly used in accurate responses and were usually combined with Consequences and Conclusions. In considering them together, they appear to have been used mainly by Year 8 students with no distinction according to gender. Distinctions according to decile level of school attended occurred with hypothetical Premises, but, in response to the Motorway task, the distinction was between Pacific and non-Pacific students. However, there were differences in the type of proof schemes produced. Hypothetical Premises were used with Consequences and Conclusions to produce empirical proof schemes, whilst mathematical Premises were developed into externally-based proof schemes. It would seem that the task requirements influenced the type of Premise necessary to achieve an appropriate response. It would also seem that not all students were able to recognise what was the most appropriate Premise to use in responding to the task. Personal Premises were used in responses to both the Bank Account and Motorway tasks. These Premises did not occur in accurate responses and did not link to any kind of proof scheme. In the Motorway task, personal Premises were most often mental processes such as 'guessed', 'think' and 'said'. In the Weigh Up task, 'think' was classified as a Supposition and was often used to lessen the certainty of what was being proposed. In responses to the Motorway task, personal Premises were more likely to be used to express uncertainty about what they had to do. Only one student combined a personal Premise with a Consequence. Students who gave these Premises were most likely to be boys in Year 4, from Pacific Island communities and attending low decile schools. If these results are considered with those for factual Premises, which also tended to be used in inaccurate responses, it would seem that these types of Premises were mostly used by Year 4 students. This probably reflects the fact that these students did not have sufficient mathematics to respond successfully to the tasks. Whereas girls tended to use factual Premises which repeated information from the question, boys, in responding to the Motorway task, tended instead to use a personal Premise. It would be interesting to know whether teachers felt that factual Premises showed that students knew more mathematics, as they often included mathematical information from the question. When examining responses for a similar NEMP mathematics task, Anthony and Walshaw (2002) found that, when students repeated parts of the question, these were accepted as explanations by the teacher administrators as no further probing was done. This may mean that boys, in being blunter about their lack of knowledge, may be perceived as knowing less and thus being given more support to improve their mathematical knowledge. In responses to the Bank Account task, personal Premises were clauses which had a person, often unspecified, as the main actor. These personal Premises were, therefore, of a different kind from those used in the Motorway task. In responses to the Bank Account task, more students used these Premises than any other kind, but more often than not they were combined with other kinds of Premises within the one response. There were no differences in the groups of students who gave this Premise. Graphical and monetary Premises were also specific to responses for the Bank Account task, as they related to the graph provided as a resource or to money respectively. The responses to the Bank Account task were the least complex and often were a series of personal, graphical and monetary Premises. Sometimes, they were combined with Consequences. As with personal Premises, there were no differences in who gave these types of Premises. Premises can be considered the grounds for an argument, but were most likely to be used in appropriate responses if they were hypothetical or mathematical. It was less likely that, if a student used other types of Premises, they would be combined with Consequences and Conclusions into complex explanations and justifications. This was because the evidence which they provided needed to be a strong foundation from which a logical train of thought could be developed. Although it would have seemed that factual Premises based on information supplied in the question or in a resource would also have provided this basis, these Premises were rarely combined with Consequences and Conclusions and used in appropriate responses. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aConsequences | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If Premises of a particular type can be considered grounds, then Consequences have the potential to match Krummheuer's (1995) warrants and backings, as they could contain the information that relates the grounds to the claims. In order to produce an acceptable mathematical explanations and justifications, it is necessary for the grounds to be manipulated in some way, so that the logical relationship to the claims is clarified. This includes identifying the conditions under which the manipulation is valid. Esty (1992) discussed the use of logical connectives in identifying the conditions for which certain mathematical statements were true. In a general sense, Consequences can be considered warrants and the way they are connected to their corresponding Premises can be considered the backings. The conditions for when a manipulation is valid is often contained within the logical connectives joining the Premises to the Consequences, as well as within Elaborators connected to Consequences. In this section, the logical connectives used in a Premise - Consequence and Consequence - Consequence are also discussed. Consequences were of two kinds; logical and Physical. Logical Consequences always described the result of a manipulation of Premises and were never used by themselves. Table 8.4 outlines who used logical Consequences in their responses to the various tasks. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.4. Use of Consequences in different tasks. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If Consequences are considered to be warrants, then it is quite clear that students felt that the explanations for some tasks required them more than others. As students moved through the Weigh Up task, more began to use Consequences so that when they gave their final explanation only five students did not use a Consequence. In regard to the different groups, there appears to be no difference in use according to gender. On the whole, Year 8 students used more Consequences than their Year 4 peers, but most of this difference is accounted for in the responses to the Better Buy task. More students attending high decile schools also used Consequences, but there were no very large differences for any particular task. In almost all tasks, Consequences combined with certain Premises were linked to responses which were considered accurate and clear. For example, in the Better Buy task, responses which combined hypothetical Premises with Consequences and Conclusions were often accurate. It was more than likely that, in responding to this task, it was a Year 8 student not attending a low decile school who used Consequences. As well, in responses to the Motorway task, there was no difference according to gender in who used Consequences, but there was also little difference between Year 4 and Year 8 students. As was seen in Table 5.6, although students attending high decile schools were slightly more likely to use Consequences than non- Pacific students, both groups were far more likely to use them than Pacific students attending low decile schools. In the Weigh Up task, there were slightly more boys who used a Consequence in their response to the Plan section. However, there were no other differences between groups using Consequences in this section. In the Description section, slightly more Year 8 students used Consequences than Year 4 students. In the responses to this section of the task, there were no differences in gender, ethnicity or school decile level. In the responses to the Explanation section of the task, there were no differences between groups who used Consequences in their responses. The distribution of logical connectives between Premises and Consequences and between Consequences suggested that the task requirements influenced their use. When a Premise began with an 'if', as was the case for hypothetical Premises, it was unlikely that another connective would be provided in front of the following Consequence. However, in long responses, such as those given for the different sections of the Weigh Up task where Premise - Consequence combinations were iterated, some students would often use several different logical connectives to join Premises and Consequences and groups of Consequences together. On the whole, it was more common for students to use narrative rather than causal connectives. However, some tasks, such as Motorway, seemed to encourage students to use more causal connectives than others. This may be because the questions in this task asked more explicitly for an explanation than the Bank Account task did. Those who were more likely to use logical connectives also seemed to change depending upon the task. When all the connectives are considered together, it was more likely that the students who used them would be in Year 8 and more probably not be attending a low decile school or not be a Pacific Islander. However, these distinctions were not always clear cut across tasks, with more Year 4 students using more logical connectives when responding to the Plan section of the Weigh Up task. Physical Consequences were the other type of Consequences. They could be found without Premises and were used mainly in responses to the Plan and the Description sections of the Weigh Up task. They described the result of a physical manipulation of the boxes and so the action itself can be considered as a silent Premise. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.5. Use of Physical Consequences in different tasks. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
As Table 8.5 shows, there was little difference in those who used Physical Consequences in the three sections of the task. As it was the same students who were giving explanations in all three sections, it is quite clear that the task requirements had a strong influence on the inclusion of these text elements. The Description section of this task required students to talk about what they were doing as they were doing it. In a shared situation where the students were physically manipulating the boxes, it is not surprising to find that Physical Consequences were the most common elements in responses. Sometimes Physical Consequences were followed by logical Consequences. In responses to the Plan section of the task, 21 students gave a Physical Consequence, but only three followed it with a logical Consequence. However, the situation changed in the Description part of the task. Of the 63 students who used Physical Consequences, 36 followed them with logical Consequences. 94% of accurate and clear responses to the Description part of the Weigh Up task contained Physical Consequences combined with logical Consequences. A considerable number used causal connectives between them, with 25 students using 'so' and a further three students using 'so then'. More causal connectives were used in this position than in any other connections between text elements. These causal connectives were most likely to be used by girls, Year 8 students and least likely by students attending low decile schools. Although fewer students attending low decile schools had used logical Consequences, the difference in causal connectives is larger. Consequences are important features in mathematical explanations and justifications, as they fill in a step from relating the information contained in the Premise to the actual claim being made. As such, they can be seen as fulling the role of warrants. However, in joining logical Consequences to Premises, it would seem that if a causal connective was used, it would be 'if' and would occur before the Premise. On the 137 whole, narrative connectives such as 'and' were most often used between Premises and logical Consequences. When Physical Consequences were used in responses to the Description part of the task, a large number of students used the causal connective 'so' to join them to logical Consequences. Research with responses to other tasks which require physical manipulation of materials needs to be done to see whether the use of causal connectives is more likely in this situation. Although Consequences could be considered equivalent to warrants, when considering how backings are linguistically represented the use of narrative rather than causal connectives limits the information about when the warrants were valid. Backings are also linguistically represented through Elaborators, as they also provided extra information about Consequences. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aConclusions | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Conclusions were text elements which were not found by themselves. On the whole they rounded off an explanation, often coming after a Premise and a Consequence. They are, in many ways the linguistic equivalent of Krummheuer's (1995) claims, as they are the outcome of the explanation or justification. As can be seen in Table 8.6, they were used in responses to all tasks, although it was only in the responses to Better Buy that more than half the students used Conclusions. This is not as surprising as it first appears. The scripts for Better Buy and Motorway both initially ask students for a result of a calculation before going on to ask for a justification and an explanation, respectively. Therefore, a repetition of this result is not necessary for the explanation to make sense. Yet, in explaining why one box is better value for money than the other, it is not unreasonable to include a second mention of the actual result. As well, some students pre-empted the second question in this task and so the Conclusion came at the beginning of the explanation as well as at the end. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.6. Use of Conclusions in different tasks. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In the Bank Account task, there was no common way for completing the story. Three students finished their responses with 'that's all', which, like all Conclusions, signalled the end, although no reference was made to the requirements of the task. The responses to each of the sections of the Weigh Up task were varied, as there were many appropriate ways to explain how to determine the order of boxes from heaviest to lightest. Given that this was so, it is fascinating to see that over a third of students provided a Conclusion in their responses to the Explanation section. It may well be that the imaginary nature of the last part of this task - 'explain it to some one else in your class' - and the fact that students were giving their third version of this explanation encouraged more students to complete their responses with Conclusions. When considering the results in Table 8.6, there appear to be few differences according to gender. In the Better Buy task, slightly more boys used Conclusions than girls, but in the Explanation section of the Weigh Up task, slightly more girls used Conclusions than boys. It would seem that Year 8 students and students at high decile schools are much more likely to use Conclusions than other groups. The large number of students who included Conclusions in their responses to the Better Buy task have had a significant effect on these results. It was also in responses to the Better Buy task that the two types of Conclusions were seen most clearly. These were implicit and explicit Conclusions. In responses to the Better Buy task, explicit Conclusions were ones which made reference to better value for money, which was what the original question had asked about. An implicit Conclusion did not make direct reference to better value, but instead made a veiled reference through using words such as 'only' or 'cheaper'. In the responses to the Better Buy task, boys and Year 8 students and students from high decile schools were more likely to use explicit Conclusions, whilst implicit Conclusions were used by equivalent numbers of boys and girls, but also by more Year 8 students and students attending high decile schools. More students used implicit Conclusions than explicit ones in this task. In the remaining task, it was not always easy to distinguish between these two types of Conclusions. However, on the whole, more implicit Conclusions were used than explicit Conclusions. This was the case in the responses to all three parts of the Weigh Up task as can be seen in Tables 4.2, 4.15 and 4.28. In these responses, students were far more likely to mention the boxes being 'in order', which was coded as implicit, than to say something about the boxes being 'in order from lightest to heaviest', which would have been coded as an explicit Conclusion. Logical connectives were also important in joining Consequences to Conclusions in responses to only some of the tasks. Given that extra information for the backing for the claims in the Conclusions could be provided in these logical connectives, it is surprising to not find them in this position in responses to all tasks. In responses to the Better Buy task, though 'and' was still the most often used connective, 6 students used 'so' and a further 5 used 'but'. These causal connectives were more likely to be used by Year 8 students (as also were the narrative connectives in this position) and least likely by students attending low decile schools. In the responses to the Plan and Description parts of the Weigh Up task, very few connectives were used between Consequences and Conclusions. In the responses to the Explanation section, 23 students used connectives, but only seven of these were causal. As had been the case with logical connectives surrounding Consequences, more girls than boys used narrative connectives. In the Motorway task, only 7 students used connectives before the Conclusion and, of these, none were causal. There were not enough Conclusions in the Bank Account task for logical connectives to be worth considering. It would seem that Conclusions were an optional element for many students when giving mathematical explanations and justifications. However, for some tasks, like Better Buy, the majority of students felt that their responses should include a Conclusion of some sort. When Conclusions were given, they were usually implicit, with the listener left to make the final jump between the speaker's response and the actual question asked. As backings are considered to be the information which defined when the claim is true, it was felt that the logical connectives would be the linguistic embodiment of these backings, particularly around Consequences. As Conclusions represented the claims themselves, it was also felt that the logical connectives around them could also constitute part of this backing. However, on the whole very few connectives were used and mostly these were narrative rather than causal. This suggests that it was uncommon for students in primary schools to use causal connectives to identify the conditions under which claims were valid. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aSuppositions | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Suppositions could not be related to any of the components of explanations described by Krummheuer (1997). Instead, this text element was used to add a propositional element. Suppositions were clauses which made preceding or following clauses propositional or more vague. As a result, they never came at the beginning or the end of an explanation. Although Suppositions were only coded within the Weigh Up task, they were also evident in responses to the Bank Account and Motorway tasks. However, they were considered as hedges and are described in the sections on hesitant language, at the end of the chapters on these tasks. In the Weigh Up task, students needed to talk about courses of action that they may take rather than those that they had taken. Using Suppositions gave students ways to discuss these possible courses of action. This enabled students to give the generic responses described by Bills and Grey (2001) which used a specific example to illustrate a general case. This is the situation in 'say if C was the heaviest you stick that, that one down at the bottom'. 'Say' was coded as a supposition, as it situates what follows as a possibility rather than a definite action. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.7. Use of Suppositions in different tasks. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 8.7 shows that there were very few distinctions across tasks. This is surprising, as the Description part of this task required the students to describe what they were doing rather than what they would be doing. It was not expected that there would be uncertainty in this. However, in responses to this part of the task, the Suppositions used were predominantly 'I think' which lessens the certainty of what was proposed, as was the case in 'I think that one there's the second heaviest'. These did not set up a proposition in the same way as 'say' did. There were some differences in the groups who used Suppositions as girls and Year 8 students used them more than other groups. It would also seem that students attending middle decile schools were slightly more likely to use them than students attending other decile levels of schools. Suppositions added uncertainty to information contained in other text elements. Sometimes they were used by students to lessen a possible loss of face, whilst at other 140 times they were used to show that an action was proposed rather than actually happening. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aElaborators | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Elaborators like Suppositions were not used in responses to all tasks. They added further information to other text elements and could be considered as contributing to backings given in mathematical arguments as sometimes the extra information was about the conditions for when the claim was valid. This can be seen in the following example: 'test for the lightest one and then put the two left overs in the middle whichever's the heaviest obviously goes that way'. 'Whichever's the heaviest' is the Elaborator and provides information which constrains what 'goes that way'. Elaborators were combined with all other text elements but they were most likely to be combined with Premises and Consequences, which were the two most commonly used text elements. Table 8.8 provides information on who used Elaborators in which task. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.8. Use of Elaborators in different tasks. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Unlike Suppositions, there do seem to be task differences in the number of students who used Elaborators. 64 out of a possible 71 students used Elaborators in the Explanation section of the Weigh Up task. As this section produced the longest, most complex responses, it would seem that Elaborators contributed to this complexity. However, the responses to the Bank Account task were also long but often the text structures were quite simple compared to those found in the responses to this section of the Weigh Up task. Only 23 students used Elaborators in the Bank Account task and these were mostly used with Premises, as can be seen in the following two tables. Tables 8.9 and 8.10 show how Elaborators were distributed with Premises and Consequences. Although some Introductions, Physical Consequences and Conclusions included Elaborators, there were so few of these that they have not been included. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.9. Use of Elaborators with Premises. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Table 8.9 shows that only in responses to the Explanation section of the Weigh Up task were Elaborators combined with Premises by the majority of students. In the other tasks, about a quarter of students combined Premises with Elaborators. When all the results are considered together, there seems to be little difference between Year 4 and 8 students or students attending different decile levels of schools. Although Premises were used equally by boys and girls, girls were more likely to combine them with Elaborators. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table
8.10. Use of Elaborators with Consequences. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
As was noted in the Weigh Up chapter, a greater proportion of Consequences were combined with Elaborators than Premises. In the responses to the Bank Account task, this was not the case. Slightly more girls than boys used Elaborators with Consequences but the distinction is quite small. There does not seem to be any distinction between age level or decile level of school attended. The results of Tables 4.14, 4.27 and 4.41 suggest that there is no clear relationship between using an elaborator with a Consequence and having a response considered clear and accurate. Elaborators were text elements which only appeared in students' responses when combined with another text element. Their role was to provide further information than was already given in the text element with which they were combined. Proportionally, they were used with Consequences more often than any other text elements. When Elaborators were combined with Consequences, they could also provide information about when the warrants given in the Consequences were valid and thus could be considered as part of the backings. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aCombining text elements | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The distribution of text elements throughout students' responses to the four mathematics assessment tasks was not random. Although there were always some exceptions, on the whole, Introductions began the responses, Premises preceded Consequences which preceded Conclusions. Suppositions and Elaborators were always combined with other elements. Premises, Consequences and Premise - Consequence combinations (with their corresponding Elaborators and Suppositions) could be iterated several times throughout a response. Figure 8.1 provides a flowchart of the possible decision making process that a student goes through subconsciously in order to provide a response to mathematical assessment tasks. This flowchart is idealised in two ways. The first is that it is unlikely that even unconsciously students would go through such a decision making process. The other way in which it is idealised is that the sort of response that such a flowchart would produce would match very few of the actual examples that were given. This is because there was so much variation in the responses. Some of this variation could be accounted for in regard to the accuracy of the responses, as certain combinations such as Premise - Consequence or Physical Consequence - Consequence combinations were more likely to be used in accurate responses. However, there were differences in the likelihood of these combinations appearing in accurate responses, depending on which task students were responding to. This suggests that there was more to knowing how to provide appropriate mathematical explanations and justifications than knowing how to combine text elements. This is discussed further in the next section. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
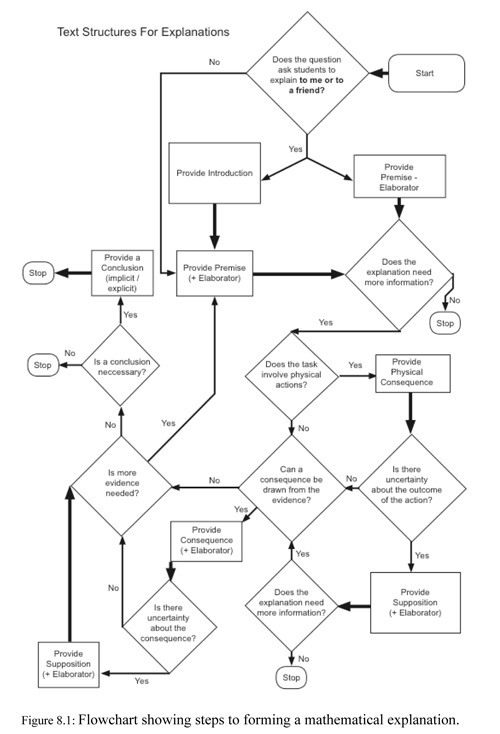 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure
8.1: Flowchart showing steps to forming a mathematical explanation. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aContextual Configuration | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
It was suggested in Figure 1.1, that in order to be assessed as accurate in responding to mathematical tasks, students need to have knowledge of mathematics and mathematical language. This research suggests that what is required is far more complex. Although most groups of students do seem to have appropriate text elements in their linguistic repertoire, these were not always used in a mathematically appropriate way. Bills (2002) had also found that, although students had certain linguistic features when discussing non-mathematical topics, they did not always chose to use them when discussing mathematical topics. Bills (2002) suggested that, when students were accurate, they were more likely to use certain features such as logical connectives. However, our research suggests that there were some students who provided accurate answers in tasks such as Motorway, but were unable to provide accurate descriptions of their thinking processes. This can be seen in the following example:
In trying to understand the variety of students' responses, the relationship between the contextual configuration and the text structure needs further examination. In cases such as shop encounters, Hasan (Halliday & Hasan, 1985) suggested that there is a clear relationship between the contextual configuration and the text structure. The compulsory text elements such as the buyer's description of what they want comes at a set place in the interaction, along with optional elements such as the vendor's enquiry about the buyer's needs. The contextual configuration was such that the roles of vendor and buyer are clearly delineated by the event of buying something, which restricts significantly what is appropriate for each participant to say. Krummheuer's (1997) description of the components of mathematical arguments suggested that certain features would be evident in mathematical explanations and justifications. This would thus also provide a clear relationship between the contextual configuration and the text structure. It would seem that Premises, Consequences, Conclusions and Elaborators can be related to grounds, warrants, claims and backings at least in a loose way. It would also seem, that in giving responses to mathematics assessment tasks, primary school children draw upon this set of text elements. However, not all of these text elements would be specific to mathematical assessments. Nor were some text elements and combinations likely to provide appropriate mathematical responses. For example, students who used personal or factual Premises were unlikely to be giving accurate responses. So what influenced students to give appropriate responses? There is a relationship between the contextual configuration and text structure and this can provide information on the stage that these students were at in giving appropriate mathematical responses. In order to act appropriately in these situations, students 144 needed first to recognise the contextual configuration that they were in and then draw upon three interconnected pieces of knowledge: appropriate mathematical knowledge; knowledge of how to interact with a teacher; and knowledge of how to structure mathematical explanations. These can be seen in Figure 8.2. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
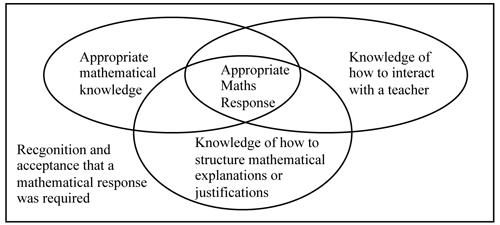 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure
8.2: Knowledge drawn upon to produce an appropriate response. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If students did not recognise that there was a need to show their mathematical knowledge in the interaction, then it is unlikely that students drew upon their knowledge of mathematics or the structure of mathematical explanations (as discussed in the previous chapter on story telling). This can be seen in the following response from the Better Buy task by a Year 4 girl from a low decile school:
This girl used many of the features of mathematical explanations such as a Premise - Consequence combination joined with causal connectives. However, the mistaken belief that the task required a description of a shopping strategy means that the response cannot be considered appropriate, as it did not show what she knew mathematically. If students recognised the purpose of the interaction as one requiring them to show what they knew mathematically, they still needed to combine their understanding in the other three areas to produce an appropriate response. The responses documented in this report suggest that it is not often a lack of knowledge of how to interact appropriately with a teacher which inhibited students' production of mathematical responses. Yet there were instances where students stated that they did not know the answer or refused to answer altogether, which could be seen as a breaking of the pragmatic rules of conversation. In the responses to the Bank Account task, of the 12 students who gave these sorts of responses, only one was from a high decile school. This task was difficult for all students, so it was interesting to see that these were not considered valid responses by students attending high decile schools. Often, these sort of responses could be seen as occurring foremost because of the students' lack of mathematical knowledge. However, this was not always the case as can be seen in the following interaction between the teacher administrator and a Year 8 boy from a high decile school:
Although his initial response is that he did not know, when questioned further by the teacher administrator, he was quite capable of doing the mathematics. It is hard to know why he chose not to show what he was capable of initially. Maybe aspects of the situation such as receiving no feedback on the accuracy of his performance confused him about what was required from him by the teacher administrator. It may be that in the classroom in which he had learnt about acceptable responses in similar situations, that confessions of ignorance were acceptable to his teacher. They, therefore, did not break the pragmatic rule of providing a response which fitted the hearer's expectations. Conversely, it may be that, although he knew what was required of him, he did not share the teacher's belief that it was necessary for him to do this. In this case, although the teacher administrator may believe the contextual configuration is fixed, the student feel that other options, such as non-compliance are available. The third area of knowledge that students need in order to provide an appropriate mathematical explanation or justification was knowledge of the appropriate text structures. The responses examined in this report suggest that acceptable responses for this age group, although drawn from a restricted set of text elements, can be extremely variable. As has been reported in each chapter, there are some text combinations, such as Premise - Consequence, which seem to be correlated with accurate and clear responses. However, in the previous example, this boy did not explain how he gained this answer clearly, even though he uses a Premise - Consequence combination joined with a causal connective. It may be that the range of proof schemes which are appropriate in primary school in responding to these different tasks encourages such diversity in text structures, even when students have sufficient mathematical knowledge. At later stages in their school careers, it may be that they are restricted to analytical proof schemes which Sowder and Harel (1998) described as 'the ultimate in justifications' and thus the text structures are also restricted. Further investigation needs to occur to determine the validity of this conjecture. When students' responses are considered holistically, it can be seen that more than just mathematical understanding and being able to structure a mathematical response is required. This includes having an awareness of what is involved in the contextual configuration and accepting it as valid. Once students have recognised and agreed on the need to show their mathematical knowledge, they then need to access and combine the appropriate mathematical knowledge, ways of interacting with a teacher administrator and knowledge of text structures of mathematical explanations and justifications. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| aConclusion | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In the responses to the different mathematical tasks, students combined a series of text elements (Introductions, Premises, Consequences, Conclusions, Suppositions and Elaborators) into text structures. Many of these text elements could be related to the 146 constituent parts that Krummheuer (1997) proposed for a mathematical argument. It was also possible to see a relationship between the type of Premise provided and the proof schemes described by Sowder and Harel (1998). This suggested that the contextual configuration had an effect on the text structures needed for an appropriate mathematical explanation and justification. The flowchart given in Figure 8.1 suggested a series of decision making points that students went through in producing their responses to the different assessment tasks. However, it was also clear that there was immense variability in the responses, so it may not just be mathematical or language ability alone which determines whether a student produced an appropriate mathematical response. It would seem that not only should the contextual configuration be recognised by both participants - the student and the teacher administrator - but also it must be accepted by the student as valid for them to then draw upon their mathematical knowledge, language knowledge and interactional knowledge. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||