The analysis of Year 4 and 8 students’ responses indicated that fractional understanding is a complex domain—understanding builds incrementally, over considerable time, as opposed to being an all-or-nothing occurrence. Many children in the NEMP study appeared quite confident with solving fraction problems with reference to the context; however, several of those who used the formal mathematics of classroom, rather than their informal knowledge, appeared confused by fraction rules and procedures.

The research reviewed in the introduction (Section 1) indicated that unlike children’s construction of early number knowledge that often occurs informally, a great deal of children’s fraction learning take place through instruction. Teaching fraction operations involves stretching and transforming the domain of numbers with new ideas such as the incommensurability of different units for addition, or that multiplication makes smaller answers rather than larger. Unfortunately, the research also suggests that much of the current instruction is relatively ineffective in terms of student learning. As recently as 2002, initial assessments of New Zealand Year 7-10 students’ in the NEST numeracy project found students in these year groups to be unexpectedly weak in knowledge of fractions:

“Many teachers were concerned at the number of their students (10% of all students) who could not identify unit fractions such as 1/4 or 1/3. A further 40% of year 9 students…could identify unit fractions but could not successfully complete stage 6 tasks, which involve ordering unit fractions…” (Irwin & Niederer, p. 47)

To suggest a single model or recipe for successfully teaching fractions would be naïve. Susan Lamon, a researcher who has invested considerable energies into investigating the teaching and learning of fractions, states that although “we have a much better understanding of the role the presenting and representing fractions in instruction plays in enabling or disabling the development of rational-number understanding” we do not have definitive answers on such issues as “which interpretations can or should be integrated in instruction” (Lamon, 2001, p. 163). In response to criticism (e.g., Behr, Wachsmuth, Post, & Lesh, 1984) that teaching practices have been dominated by experiences of part-whole representations, with only passing attention to alternative subconstructs, Lamon contends that teachers must move froward from the part/whole constraint, which retains a focus on the relative amount, to more frequent use of part/whole interpretation with unitising
[Unitising refers to the cognitive process of reconceptualizing a quantity according to some unit of measure that is convenient for thinking about and operating on, the quantity. For example, the given unit in a fraction problem may be 12 cans of drink, but a student may think about that quantity as 1 (12-pack), 2 (6-packs), 3 (4 packs) etc. (see Lamon, 1999 for more instructional examples)] and the measure interpretation:

Both rely heavily on the principles of measurement—the inverse relationship between the size of the unit with which one is measuring and the number of times one can measure it, out of a given quantity, and the successive partitioning of that unit of measure into finer and finer subunits until one can name the amount in a given quantity. (p. 163)

Lamon’s research suggests that the unitising and measure interpretations and their corresponding representations assist children to make the transition from whole numbers to rational numbers because these interpretations build on and extend principles of measurement with which the children have been familiar since early childhood. Other researchers (e.g., Empson, 2002; Mack, 1993) also propose that partitioning and equal sharing are effective starting points as they provide explicit links with a range of children’s informal knowledge situations.

Use of informal knowledge
While “instruction to assist students in extending and building on their informal knowledge of rational numbers cannot be prescribed precisely” (Mack, 1993, p. 95) it is clear that the range of suggested approaches all utilise young children’s capabilities for mathematical thinking and knowledge construction (Carpenter et al., 1993). Engaging children in purposeful, meaningful, and inquiry-based instruction that integrates their informal knowledge with the instructed knowledge can capitalise on the need for fractions and the development of actions sequences about fractions that arise quite early in children’s everyday social activities (Kieren, 1988; Perry & Dockett, 2002; Smith, 2002). To achieve the ultimate goal of fraction instruction, that is, that students understand fractions as numbers in their own right, there are some agreed fundamental activities that can serve children’s initial reorganisation of fraction conceptions: equidivision of wholes into parts (sharing), recursive partitioning of parts (splitting), and reconstruction of the unit (i.e., the whole) (Pitkethly & Hunting, 1996). For example, using scarce or desirable objects like biscuits or lollies within contexts involving division of an object or group of objects amongst friends provides the basis for invented strategies for equal-sharing problems (Sharp, Garofalo, & Adams, 2002).

In order to acknowledge the initial resources for thinking about fractions that children bring to the classroom, teachers need to select a representational domain which is familiar and understandable to the childrenæin other words, a domain in which they can extend and develop their understanding of the ideas, as well as their capacity to reason with and about those ideas (Ball, 1993; Carpenter et al., 1993; Mack, 1990, 1998). The teacher’s role is to select and construct appropriate models, examples, stories, illustrations and problems. In the NEMP study the problems involved a pizza context: many students used the pieces of pizza to explain their thinking, and in some cases the pieces of pizza were needed to support the children’s thinking. The Year 4 students, in particular, tended to largely rely on their informal knowledge of whole number counting rather than fraction schema to interpret the problems. For example, in response to the question “How much of the pizza is left?” the link between 3 pieces of pizza and _ of a pizza was tentative, and needed prompting by the interviewer.

As children learn, they develop more intuitive knowledge in which they combine thought, informal language, and images; they become more able to extract mentally, and think about, fractional ideas without a strong dependence on the specific context. Those students who were readily able to switch back and forth between reasoning with whole numbers and naming the fractional number indicated that their fractional and whole number sequences had achieved similar levels of abstraction (Olive, 2002).

One of the critical actions in building rational knowledge is the matching of problems presented in the context of familiar situations to symbolic representations. Mack (1993) suggests that in order to promote connections between the symbolic representation and informal knowledge teachers need to make frequent adjustment of problems to make those that draw on informal knowledge and those that are presented symbolically more similar. While there is no doubt that, eventually, children should be able to express their mathematical ideas using the standard mathematical symbols it is unnecessary, and even counterproductive, to expect sophisticated symbol use among young children — who often have developed their own system of symbols and can use this consistently — until another more standardized system can be taken on board (Hughes, 1986). To facilitate meaning for symbols and formal mathematical language connections must be made between students’ conceptual understanding and informal language — it is important that the meanings make sense in an interconnected manner and originate in children’s thinking about things they understand (Hiebert et al., 1997). Empson (2001) for example, notes that moving children from solving 24 children sharing 8 pancakes to 8/24 = 1/3 takes time, and is assisted if concepts such as equivalence, multiplication and division are allowed to develop concurrently.

The NEMP study findings showed that some students had developed separate systems of arithmetic that operated independently of one another—an informal system that they used to solve problems that are meaningful to them and a school arithmetic system that consisted of procedures that they applied to the apparently artificial story problem presented to them. These systems were especially evident in relation to Questions 5 and 6 when answered by Year 8 students using an algorithmic procedure that did not relate to their verbal explanation/demonstration of the successive partitioning of pizza pieces. However, within a classroom situation, a teacher can use these instances as teachable moments to assist students to recognise the connection between the symbolic representation and the student’s informal knowledge. For example, in Question 5 and 6 the student’s meaningful strategy of sharing can be used to provide an initial context for solving the symbolic problem of 1/2 x 11/4 or 11/4 ÷ 2 as well as providing a context for discussing equivalent fraction concepts. Building on the match between students’ reasoning of the problem presented in the context of the familiar situation will help students to connect their informal knowledge for rational numbers with the corresponding symbols and procedures.

Influence of Context and Representations
When assisting students to link their informal knowledge with symbolic representations the influence of context is significant. For example, a commonly reported example of how real-world concerns can collide with the mathematical viability of a representation concerns the problem of whether 3/3 is greater than, less than, or the same amount as 5/5? With reference to a ‘cookie’ context, some children argue that 3/3 is more because each piece (one third) is bigger. Others argue that 5/5 is more because there are more pieces. Still others argue that they are the same because each represents one whole brownie. However, rather than be concerned about the influence of problem contexts, teachers can and should take advantage of the fact that problem contexts can suggest representations for students to reason with directly — especially in the initial stages of developing fraction understanding.

The analysis of responses in this study clearly illustrates the influence of problem context on the students’ reasoning and eventual solution. As a representational context the pizza problem provided a ‘thinking space’ for students. Year 4 students, in particular, frequently solved the problems by referring to the constraints, real or imagined, of the context (e.g., sharing both types of pizza (ham and pepperoni), rather than all of the pizza), and provided solutions in the format of the context (e.g., number of pieces of pizza) rather than the fractional format. For the majority of students the sharing activity, invoked by informal partitioning strategies, was an integral part of the solution. Moreover, even when Year 8 students appeared to use a more formal mathematical procedure to solve the problem (in only a few cases in Question 5), they more often resorted to an informal ‘sharing type’ explanation (Question 6) that involved distributing the available pizza pieces. These findings parallel those of other researchers investigating children’s fraction problem solving involving real contexts (Kieren, 1988; Mack, 1990) and children’s problem solving in everyday settings (Carraher et al. 1987; Lave & Wenger, 1991).

Sharing problems (e.g., sharing 2 biscuits between 2 people, and then between 3 people, etc.) have been found to provide useful contexts for which children can effectively build their own models and representations of real-world phenomena as well as of mathematical ideas (Empson, 2002; Streefland, 1993). Some examples of sharing problems are found in the Teaching Fractions, Decimals, and Percentage Numeracy booklet (Ministry of Education, 2003a). Equal sharing provides a productive context for several reasons: Firstly, equal sharing relates well to children’s informal knowledge of partitioning strategies (Carpenter et al., 1993), and can be used in both continuous and discrete contexts. Secondly, the used of equal-sharing contexts facilitates varied mathematical interpretations by children, a key to cognitive change in joint activity (Streefland, 1993). Initially, the most salient aspect of sharing involves the action of partitioning; the size of the resulting pieces and the relationship between the number of sharers and number of shared units are of secondary importance. However, extending the problems to involve ‘fair or equal’ shares encourages the necessity of parts of equal size; same number, and exhaustion of the whole. Rational number subconstructs that are exposed in equal-sharing situations include partitioning, part-whole, and ratio. Part-whole concepts arise in the context of partitioning and discussing the resulting pieces and their size relative to a discrete unit (e.g., dividing each pizza into fourths and assigning 3 of them to obtain a value of 3/4 of a pizza). Ratio-related constructs result from conceptualising the number of people sharing and number of items shared as a composite unit (e.g., recognising that when dividing 3 pizzas among 4 people, each will receive 3/4 of a pizza).

Whatever context that is chosen, selected problems need to be sufficiently open to afford students opportunities to explore and make conjectures and follow important mathematical tangents; encouraging learners to confront and grapple with the conceptual complexity that is inherent in learning fractions. Additionally, the student needs to be familiar, and preferably interested, with the selected context — that is, the context needs to be experientially real to the learner who can then draw on his or her informal knowledge to develop an effective strategy to solve the problem (Gravemeijer, 1997b). As noted in Section 1.3 not all contexts hold equal appeal for all students. As with Mack’s (1993) finding that some children preferred ice-cream contexts to pizza, it was evident that some children in this study were ‘interested’ in the context and models provided, and several took the opportunity to comment on their pizza flavour preference!

One warning in relation to the use of contexts that teachers need to be aware of is that in our efforts to link problems to everyday experience we sometimes create contextual problems that do not in fact ‘match’ reality in a practical sense. For example, consider the following Fraction question suggested in the NumPA diagnostic test (Ministry of Education, 2002, p. 18):

Q.35 Show the student the fraction card 8/6. Pizza Picasso cuts their pizzas into sixths. You buy eight sixths (pointing to 8/6). How much pizza would you get?

From our analysis of the NEMP task it is likely that many students in the middle years of schooling would reference their informal contextual knowledge. However, in this instance, there is a possibility for confusion: it is very unusual to buy (or even ask) for eight sixths. If buying by the piece, which would not normally be the experience of most students, you would buy 8 pieces. The analysis of the NEMP task suggests that many students who are at the stage of referencing their informal knowledge would answer “eight sixths or 8 pieces” and require a lot of prompting to provide the information that is being sought in this question (designed to assess students’ ability to coordinate numerators and denominators and explain the meaning of improper fractions).

Teachers and students often represent realistic contexts as concrete or pictorial representations, for example circles for pizzas, counters or Unifix cubes for biscuits etc. These physical representations serve as useful tools for mathematical communication, thought, and calculation, allowing personal mathematical ideas to be externalised, shared, and preserved. In order to help clarify ideas in ways that support reasoning and build understanding any representation should highlight the conceptual dimensions of the content, not just its surface or procedural characteristics (Meyer et al., 2001). As was evidenced in this study the students appeared to be familiar with the exemplifying objects and were able to use familiar language to describe and communicate relations among the objects (Ball, 1993). However, the familiarity also created questions related to the social and cultural appropriateness (e.g., sharing meals in a family situation) for all children.

Representations are metaphorical, borrowing meaning from one dominant context to clarify or illuminate something in another, and thus, no one representational context is perfect. While not definitive in which representations should be used, in which order, researchers unanimously urge teachers to pose tasks that will elicit a variety of strategies and representations involving multiple interpretations of fraction symbols and concepts. Learning a “new concept is the product of a cross-breeding between several metaphors rather than a single metaphor” (Sfard, 1997). For example, equivalence, a source of difficulty for many children, can be explored in many different ways: e.g., equivalence in area, use of paper folding, multiplication by identity, decimal representations, are some. Similarly, a standard region model [see Fraction Exemplar example] is a typical representation of 1/3 — however, students should also examine mixtures of discrete and continuous representations involving more than 3 equal pieces, as well as ratio representations.

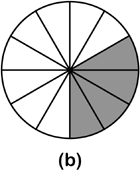(a) A discrete representation, (b) part-whole representation, and (c) a discrete representation

Helping children to recognise the multiple personality of a rational number is a challenge, but their ability to detect nuances in a range of problems and to build meaning when they have no rules or algorithms are strengths that instruction might exploit.

Within the classroom, representational contexts are co-constructed and developed by members of the class. Typically, students enter the representational context that the teacher has established and, in dealing with a specific problem, they generate alternative ways to represent or check their understandings. However, when using manipulative materials, like Fraction Tiles and fraction strips we should be cautious when linking children’s representations with pre-partitioned materials to their ability to construct and reason about their own work (Smith, 2002). Students’ work with manipulative materials does not automatically generate mathematical knowledge (Ball, 1993; Stacey, Helme, Archer, & Condon, 2002). Fraction manipulative materials skilfully used by teachers can support children’s developing knowledge of fractions, but only when these materials are seen as representations of numerous examples of divided quantities experienced previously by children. In order to reach beyond and across specific situations to abstract and generalise emergent understandings students must be supported to communicate, negotiate and reappraise their own understandings in response to the mathematical norms and values of the classroom (Anthony & Walshaw, 2002).

next page