The graphs and figures that illustrate the derivation of a hierarchical cluster profile based on the Algebra B Sample tasks follow.
The initial cluster solution is illustrated below in Figure 22 shaded at the 7 cluster solution.
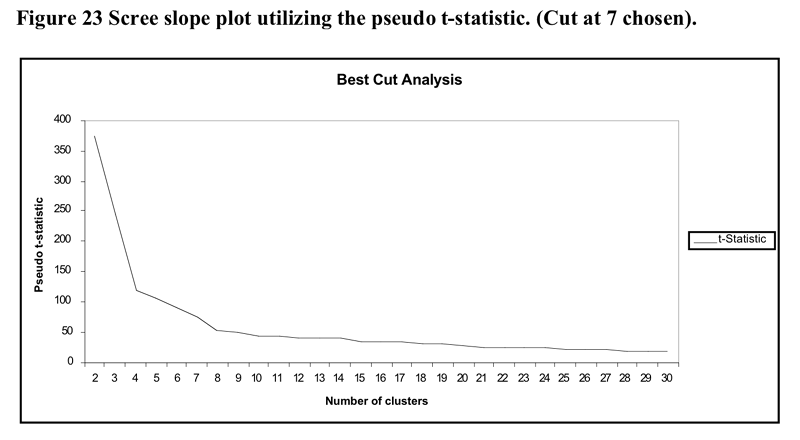
The heirarchical cluster solution was based upon the flexible cluster procedure with beta set to .25. There were 19 cases removed from the analysis due to the extent of missing data. The scree slope of the pseudo t statistic which led to the decision to utilise the seven cluster solution is illustrated in Figure 23 below. The flattening out of the pseudo-t line past the 7 cluster point may be because the amalgamations between clusters past that point do not represent joinings between profoundly different clusters.
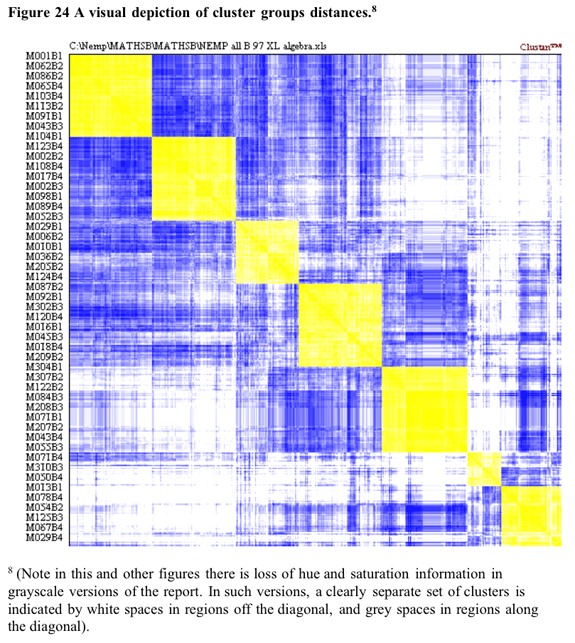
Some support for the seven cluster solution is found in the visual depiction of cluster solutions in Figure 24 below. Coloured versions of the figure showed that in general there tended to be a higher colour density within clusters than between clusters. This is particularly evident for the densities between clusters 1 and 2 and the other 5 clusters. The structure evident in the truncated tree in Figure 25 also indicates a reasonable level of separation between clusters 1,2,3 and clusters 4,5,6,7.
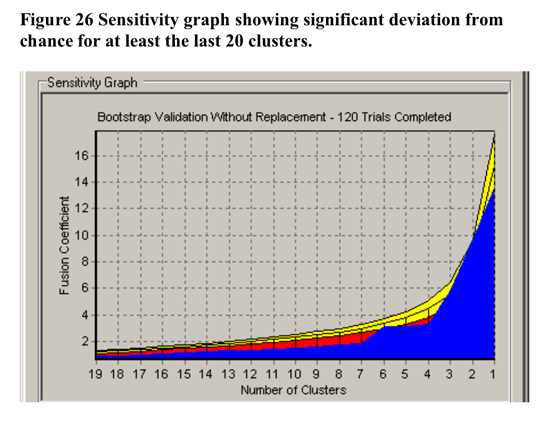
In terms of validation of the non-randomness of the cluster solution at 7 clusters, CLUSTAN GRAPHICS allowed the comparison of the series of fusion coefficients (distances) of the actual sample cluster pairs compared to a series of Bootstrap-derived sample cluster pairs. The results of this comparison is detailed in Figure 26 below. The largest deviations of the Bootstrap derived samples from the other samples is at 7 clusters. Based upon these results, the decision to utilise the 7 cluster solution in further analysis has justification.
Qualitative
Summary of cluster groups
Cross
tabulation of each task by the cluster groups was carried out. The tables
from these analyses are found in Appendix IX. For most tasks there was
a significant chi-square statistic indicating non chance differences
in the distributions of task responses between groups. A qualitative
summary of the cluster group profiles obtained by the cross tabulation
of each algebra Nemp task by cluster group follows:
Cluster group 1 showed a good grip on all tasks. They scored
lowest on their ability to utilise quasi-equations to solve problems
(for instance to write out a rule, or to solve the matchstick task of
“how many squares in the tenth matchstick building?”). All
other groups had profound difficulties with these problems. We might
label this group the algebra competent group.
Cluster group 2 had great difficulty in stating rules for obtaining
a number pattern and also in applying the rules to generate sequence
members. They were out-performed by all other groups on these items.
(It is possible that they had difficulties in understanding instructions
because even on the most basic multiplication task they had difficulty
completing sequences). Cluster group 2 however performed well relative
to all later clusters on the matchsticks task and in calculation of
Newspapers delivered in 5 days and also the cost to rent a motorcycle.
We might label this group contextual algebra facile but non symbolic
group.
Cluster group 3 was not as contextually facile as cluster group
2 but still scored well in the contextual tasks. The cluster group was
distinguishable by firstly their ability to complete number sequences
(their identification of algebraic rules was poor though), and also
by their poor performance on the consecutive operations task (particularly
when they had to carry out the reverse sequence of operations). We might
label this group the contextual algebra facile with poor operational
knowledge group.
Cluster group 4 was distinguishable from the previous three groups
by firstly their poorer ability to complete number sequences (their
identification of algebraic rules was also poor ). Further relative
to the earlier three groups they performed poorly on the contextualised
tasks (although not much worse than group three in the matchstick task).
We might label this group the operations competent contextual algebra
non-facile group.
Cluster group 5 performed very poorly on all tasks with the exception
of the number of papers delivered in 5 days. Perhaps for these children
that problem was an example of "street mathematics" (c.f.
Saxe, 1988). We might label this group the algebra non-facile “street
maths” group.
Cluster group 6 performed moderately poorly across the range of tasks apart from the consecutive operations task (which they performed well in). Interestingly, they seemed to do poorly on representing the number of papers delivered in 5 days task - which they performed poorly in. Because of their intermediate performance in a number of tasks we might label them as the transiting to algebraic symbolism group.
Cluster
group 7 performed poorly on all tasks. Their response to the number
of papers delivered in 5 days task was utilise the x + 5,
or the x ÷ 5 answer options. This along with
them being one of only two groups to do very poorly in the rent a motorcycle
task suggests a very limited acquisition of algebraic schema in these
65 students. We might label this group the completely algebra non-facile
group.
Global summary
While on some individual tasks correct performance on Algebra/Logic
tasks averaged 50%, this masks the fact that 6 out of 7 cluster groups
had particular difficulties and all groups showed difficulties using
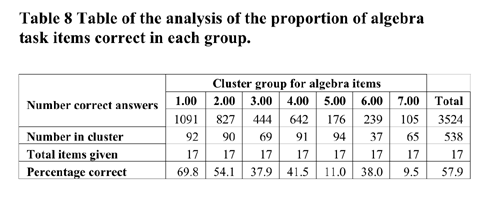
symbols to express rules. Table 8 shows that cluster group 5 and 7 comprising
30% of the total sample were floundering at algebra tasks. In essence
almost one third of year 8 students were performing not just below level
4 of the curriculum achievement objectives, but barely at level two
of the Mathematics Curriculum achievement objectives.
Some particular difficulties identified in the qualitiative analysis
were that there is a cluster of students who show difficulties in understanding
the utility of the reversal of operations in obtaining solutions, there
is a cluster of students who have particular difficulty in completion
of non-contextualised number sequences and conversely there is a cluster
of students who have greater difficulty in contextualised algebra. The
value of cluster analysis is in identifying these particular difficulties
each associated with some groups and not with others. While examination
of the total scores of students would reveal the extent of poorly performing
students, the particular difficulties of groups of students can not
be obtained by such an approach.
